Равносильные уравнения. Рациональные уравнения
| Два уравнения называют равносильными, если они имеют одни и те же корни или каждое из уравнений не имеет. |
Примеры:
1) Уравнения 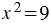 и
и 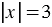 равносильные, так как каждое из них имеет два корня 3 и
равносильные, так как каждое из них имеет два корня 3 и 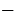 3.
3.
2) Уравнения 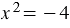 и
и 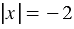 равносильные, так как каждое из них не имеет корней.
равносильные, так как каждое из них не имеет корней.
3) Уравнения 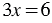 и
и 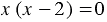 не являются равносильными, так как первое уравнение имеет один корень
не являются равносильными, так как первое уравнение имеет один корень 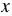 = 2, а второе уравнение имеет два корня
= 2, а второе уравнение имеет два корня 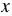 = 0 и
= 0 и 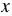 = 2.
= 2.
Преобразования данного уравнения с помощью которых можно получить уравнение, ему равносильное:
1) если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному;
2) если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному;
3) если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
| Уравнение, левая и правая части которого являются рациональными выражениями, называют рациональными. |
Пример: 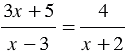 - рациональное уравнение.
- рациональное уравнение.
Запомните, уравнение вида 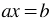 , то есть линейное уравнение с одной переменной, является рациональным, так как любое выражение можно представить в виде дроби со знаменателем, равным единице.
, то есть линейное уравнение с одной переменной, является рациональным, так как любое выражение можно представить в виде дроби со знаменателем, равным единице.
Рассмотрим рациональное уравнение вида 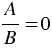 , где А и В - многочлены.
, где А и В - многочлены.
Нам уже известно, что дробь равна нулю только в том случае, когда ее числитель равен нулю, а знаменатель отличен от нуля. Следовательно, чтобы решить уравнение вида 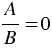 , нужно потребовать одновременного выполнения двух условий:
, нужно потребовать одновременного выполнения двух условий: 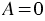 и
и 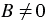 . Тогда при решении уравнения указанного вида следует использовать такой алгоритмом:
. Тогда при решении уравнения указанного вида следует использовать такой алгоритмом:
- решить уравнение
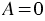 ;
; - проверить, какие из найденных корней удовлетворяют условию
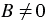 ;
; - корни, удовлетворяющие условию
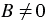 , включить в ответ.
, включить в ответ.
Получается, решение уравнения вида 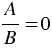 равносильно системе:
равносильно системе:
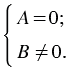
Примеры:
1) Решите уравнение 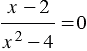 .
.
Решение данного уравнения равносильно системе:
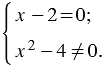
Из первого уравнения системы мы получаем 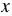 = 4.
= 4.
Во втором уравнении системы сначала в левой его части применяем формулу разности квадратов двух уравнений. Тогда рассматриваемую систему можно записать так:
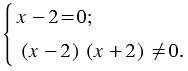
Далее во втором уравнении системы учитываем то, что произведение не равно нулю, когда ни один из множителей этого произведения не равен нулю. Тогда система примет следующий вид:
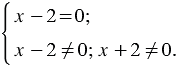
Из уравнения 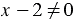 получаем
получаем 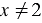 , а из уравнения
, а из уравнения 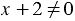 получаем
получаем 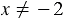 . Тогда систему можем записать так:
. Тогда систему можем записать так:
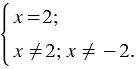
Получается, корень 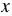 = 2, при котором числитель равен нулю, не может быть корнем рассматриваемого уравнения, так как в таком случае знаменатель обращается в ноль, чего не может быть, следовательно, данное уравнение не имеет корней.
= 2, при котором числитель равен нулю, не может быть корнем рассматриваемого уравнения, так как в таком случае знаменатель обращается в ноль, чего не может быть, следовательно, данное уравнение не имеет корней.
2) Решите уравнение 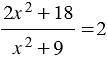 .
.
Сначала в числителе дроби, стоящей в левой части рассматриваемого уравнения, вынесем за скобки общий множитель 2, получим:
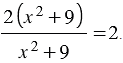
Далее учитывая то, что знаменатель дроби 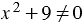 при любом
при любом 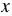 , т.к.
, т.к. 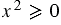 при любом значении
при любом значении 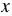 можем сократить дробь, стоящую в левой части уравнения, на общий множитель
можем сократить дробь, стоящую в левой части уравнения, на общий множитель 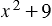 , получим:
, получим:
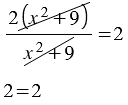
Мы получили, что рассматриваемое уравнение является тождеством, следовательно, корнем этого уравнения может быть любое число, то есть 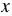 - любое число.
- любое число.
3) Решите уравнение 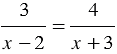 .
.
Перенесем выражение, стоящее в правой части данного уравнения в левую часть, изменив при этом его знак, получим:
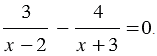
Далее представим левую часть этого уравнения в виде рациональной дроби. Для этого выполним сложение дробей.
Общим знаменателем складываемых дробей может быть выражение 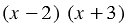 . Тогда первую дробь нужно умножить на дополнительный множитель
. Тогда первую дробь нужно умножить на дополнительный множитель 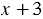 , а вторую - на дополнительный множитель
, а вторую - на дополнительный множитель 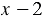 , получим:
, получим:
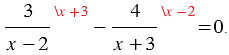
Откуда по правилу сложения рациональных дробей с одинаковыми знаменателями имеем:
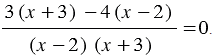
Теперь, используя распределительное свойство умножения, в числителе полученного дробного выражения раскрываем скобки, получаем:
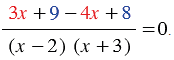
Далее в числителе полученного дробного выражения приводим подобные слагаемые (выделены одинаковым цветом), имеем:
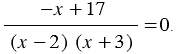
Решение данного уравнения равносильно системе:
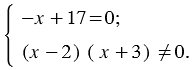
Из первого уравнения системы получаем 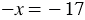 . А во втором уравнении системы учитываем то, что произведение не равно нулю, когда ни один из множителей этого произведения не равен нулю. Тогда система примет следующий вид:
. А во втором уравнении системы учитываем то, что произведение не равно нулю, когда ни один из множителей этого произведения не равен нулю. Тогда система примет следующий вид:
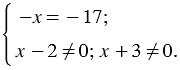
Из уравнения 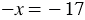 получаем
получаем 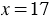 . Из уравнения
. Из уравнения 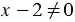 получаем
получаем 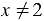 . Из уравнения
. Из уравнения 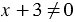 получаем
получаем 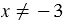 . Тогда систему можно записать так:
. Тогда систему можно записать так:
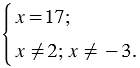
Получается, корень 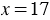 , при котором числитель равен нулю, является корнем рассматриваемого уравнения, так как в таком случае знаменатель не обращается в ноль (корни числителя и знаменателя не совпадают).
, при котором числитель равен нулю, является корнем рассматриваемого уравнения, так как в таком случае знаменатель не обращается в ноль (корни числителя и знаменателя не совпадают).
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 215, Мерзляк, Полонский, Якир, Учебник
Номер 216, Мерзляк, Полонский, Якир, Учебник
Номер 220, Мерзляк, Полонский, Якир, Учебник
Номер 221, Мерзляк, Полонский, Якир, Учебник
Номер 12, Мерзляк, Полонский, Якир, Учебник
Упражнение 634, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 641, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 657, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1300, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1100, Макарычев, Миндюк, Учебник
9 класс