Умножение и деление рациональных дробей. Возведение рациональной дроби в степень / Рациональные выражения / Алгебра / Справочник по математике 5-9 класс

Мы знаем правила умножения и деления обыкновенных дробей, рациональные дроби умножаются и делятся аналогично.

Произведением двух рациональных дробей является рациональная дробь, числитель которой равен произведению числителей данных дробей, а знаменатель - произведению их знаменателей.

Чтобы умножить одну рациональную дробь на другую, надо числитель первой дроби умножить на числитель второй дроби, а знаменатель первой - на знаменатель второй, первое произведение записать в числитель, а второе - в знаменатель.

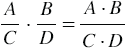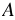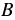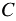, где , , и 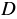- многочлены, причём многочлены 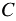и 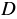- ненулевые.

Пример 1: Найдите произведение дробе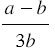й и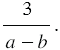

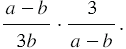
Так как числитель первого множителя равен 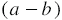, а числитель второй - 3, то числитель произведения будет равен 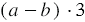. Знаменателем первого множителя является одночлен 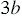, а второго - многочлен 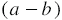, поэтому знаменатель произведения будет равен 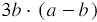, то есть получаем:

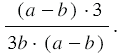
Очевидно, что нашу дробь мы можем сократить на 3 и на многочлен 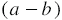, получаем, что:

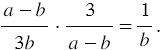
Две рациональные дроби, произведение которых равно 1, называют взаимно обратными.

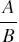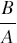То есть рациональные дроби и , где 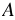, 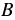- ненулевые многочлены, являются взаимно обратными, так как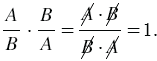

Частным двух рациональных дробей является рациональная дробь, числитель которой равен произведению числителя делимого и знаменателя делителя, а знаменатель - произведению знаменателя делимого и числителя делителя.

То есть, чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.

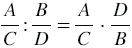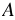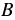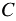, где , , и 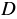- многочлены, причём многочлены 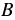, 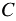и 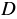- ненулевые.

Пример 2: Найдем частное дробей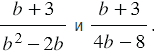

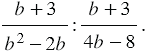
Сведем деление к умножению. Обратной дробью делителю будет дробь 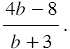Значит, мы должны дробь 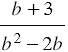умножить на дробь 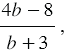получаем произведение:

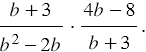
Далее в числитель произведения записываем произведение числителей данных дробей, а в знаменатель - произведение знаменателей, то есть:

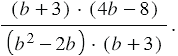
Мы видим, что числитель и знаменатель дроби содержат множитель 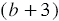, поэтому мы можем сократить данную дробь на него. Также мы можем в числителе дроби вынести за скобку общий множитель 4, а в знаменателе множитель - 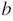, получим:

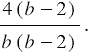
Мы получили, что числитель и знаменатель дроби содержат множитель 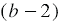, поэтому мы можем сократить данную дробь на него, в итоге имеем, что:

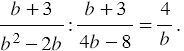
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель и знаменатель. Первый результат записать как числитель, а второй - как знаменатель дроби.

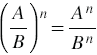, где 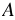, 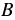- многочлены, причём многочлены 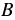- ненулевой.