Рациональные дроби
Ранее мы познакомились с целыми выражениями, то есть выражениями, составленными из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля. Так, например, к целым выражениям относятся выражения
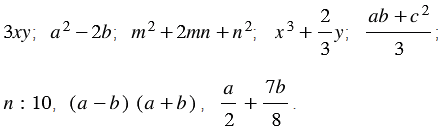
Теперь рассмотрим дробные выражения.
Дробные выражения - это выражения, которые кроме действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Так, например, к дробным выражениям относятся выражения
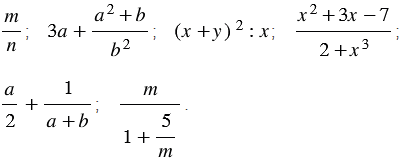
Целые и дробные выражения называют рациональными выражениями.
Если в целом выражении заменить переменные числами, то получим числовое выражение, которое всегда имеет смысл, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Если в дробном выражении заменить переменные числами, то получим числовое выражение, которое может не иметь смысла, если эта замена приводит к делению на нуль, т.к. на нуль делить нельзя.
Например, выражение  при
при 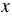 = 3 не имеет смысла, то есть не существует числового значения этого выражения при
= 3 не имеет смысла, то есть не существует числового значения этого выражения при 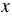 = 3. При всех остальных значениях
= 3. При всех остальных значениях 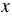 это выражение имеет смысл.
это выражение имеет смысл.
Определение:
| Допустимыми значениями переменных, входящих в рациональное выражение, называют все значения переменных, при которых это выражение имеет смысл. |
Так, в рассмотренном выше выражении допустимыми значениями переменной 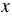 являются все числа, кроме 3.
являются все числа, кроме 3.
Допустимыми значениями переменных, входящих в целое выражение, являются все числа.
Среди рациональных выражений можно выделить отдельный вид выражений - рациональные дроби или еще их называют алгебраические дроби.
Рациональная дробь (алгебраическая дробь) - это дробь, числитель и знаменатель которой - многочлены. При этом помним то, что числа и одночлены считают отдельным видом многочленов.
Примерами рациональных дробей служат дроби
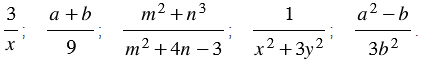
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
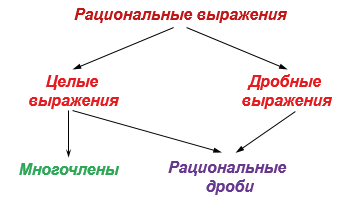
Схематично связь между рациональными выражениями, многочленами, целыми выражениями, дробными выражениями и рациональными дробями можно изобразить так:
Пример. Найдите допустимые значения переменной, входящей в выражение 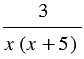 .
.
Решение:
Чтобы найти, при каких значениях 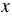 знаменатель рассматриваемого выражения обращается в нуль, т.е. значения переменной, при которых выражение не имеет смысла, нужно решить уравнение
знаменатель рассматриваемого выражения обращается в нуль, т.е. значения переменной, при которых выражение не имеет смысла, нужно решить уравнение 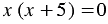 . Учитывая то, что произведение равно нулю, если хотя бы один из множителей равен нулю, это уравнение имеет два корня
. Учитывая то, что произведение равно нулю, если хотя бы один из множителей равен нулю, это уравнение имеет два корня 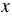 = 0 и
= 0 и 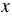 =
= 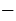 5, т.к.
5, т.к. 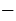 5 + 5 = 0.
5 + 5 = 0.
Следовательно, допустимыми значениями переменной 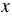 в рассматриваемом выражении являются все числа, кроме 0 и
в рассматриваемом выражении являются все числа, кроме 0 и 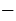 5.
5.
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 55, Мерзляк, Полонский, Якир, Учебник
Номер 132, Мерзляк, Полонский, Якир, Учебник
Номер 361, Мерзляк, Полонский, Якир, Учебник
Номер 773, Мерзляк, Полонский, Якир, Учебник
Номер 937, Мерзляк, Полонский, Якир, Учебник
Упражнение 97, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 129, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 215, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 249, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс