Степень с целым отрицательным показателем
Для любого числа 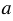 , не равного нулю, и натурального числа , не равного нулю, и натурального числа 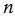 справедливо равенство: справедливо равенство: 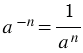 . . |
Например:
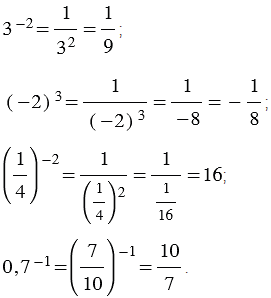
Обратите внимание, равенство 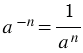 означает, что числа
означает, что числа 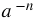 и
и 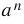 - взаимно обратные и их произведение равно 1.
- взаимно обратные и их произведение равно 1.
Для любого числа 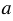 , не равного нулю, , не равного нулю, 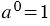 . . |
Например:
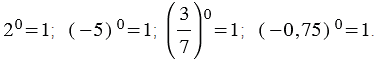
Обратите внимание, выражения 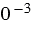 и
и 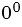 не имеют смысла.
не имеют смысла.
Если 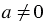 и и 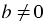 , то , то 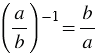 . . |
Например:
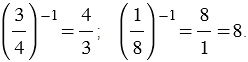
Если 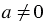 и и 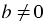 , то , то 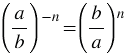 . . |
Например:
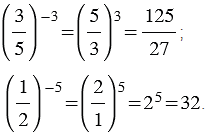
Стандартный вид числа
Стандартным видом числа называют его запись в виде произведения 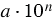 , где , где 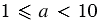 и и 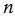 - целое число. Число - целое число. Число 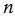 называют порядком числа, записанного в стандартном виде называют порядком числа, записанного в стандартном виде 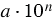 . . |
В стандартном виде можно записать любое положительное число.
Чтобы представить число в стандартном виде, необходимо помнить следующие правила:
- если нам нужно привести к стандартному виду число большее или равное 10, нужно в его записи перенести запятую влево на
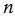 цифр и результат умножить на 10 в степени
цифр и результат умножить на 10 в степени 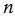 (если число записано без запятой, то ее мы подразумеваем у этого числа на конце справа). Например, 3400 = 3,4
(если число записано без запятой, то ее мы подразумеваем у этого числа на конце справа). Например, 3400 = 3,4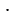 103; 6 500 000 = 6,5
103; 6 500 000 = 6,5 106 ;
106 ; - если нам нужно привести к стандартному виду число меньшее 1, нужно в его записи перенести запятую вправо на
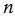 цифр и результат умножить на 10 в степени
цифр и результат умножить на 10 в степени 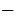
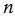 . Например, 0,0046 = 4,6
. Например, 0,0046 = 4,6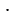 10-3; 0,000008 = 8
10-3; 0,000008 = 8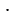 10-6;
10-6; - если нам нужно привести к стандартному виду число меньшее 10, но большее или равное 1, то это число нужно умножить на 10 в нулевой степени. Например, 2 = 2
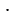 100; 3,45
100; 3,45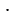 100.
100.
Заметим, что на практике стандартный вид числа обычно используют для записи больших и малых значений величин. При этом порядок числа дает представление о величине. Например, если порядок некоторого числа 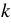 равен 5, то есть
равен 5, то есть 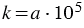 , то учитывая то, что
, то учитывая то, что 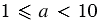 , получаем:
, получаем: 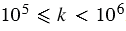 .
.
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 277, Мерзляк, Полонский, Якир, Учебник
Номер 299, Мерзляк, Полонский, Якир, Учебник
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 874, Мерзляк, Полонский, Якир, Учебник
Упражнение 1173, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1200, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1209, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1230, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1249, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1264, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс