Упражнение 253 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 86

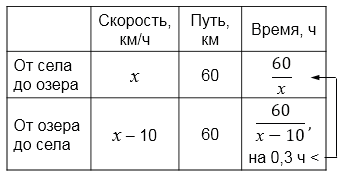
Составим уравнение:

\( \frac{60}{х - 10} - \frac{60}{х} = 0,3\) \(/\times 10x(x - 10)\)

ОДЗ: \(x \ne 0\)  и  \(x - 10 \ne 0\)

                          \(x \ne 10\)

\(600x - 600(x - 10) = 3x(x-10)\)

\(\cancel{600x} - \cancel{600x} + 6000 = 3x^2 - 30x\)

\(3x^2 - 30x - 6000 = 0\)   \(/ : 3\)

\(x^2 - 10x - 2000 = 0\)

\(a = 1\),  \(b = -10\),  \(c = -2000\)

\( D =b^2 - 4ac =\)

\(= (-10)^{2} - 4 \cdot1 \cdot (-2000) =\)

\(=100 + 8000 = 8100. \)

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\),    \(\sqrt{D} = 90\).

\(x_1 = \frac{10 + 90}{2\cdot1} = \frac{100}{2} = 50 \).

\(x_2 = \frac{10 - 90}{2\cdot1} = \frac{-80}{2} = -40 \) не удовлетворяет условию.

1) \(50\) км/ч - скорость от села до озера.

2) \( 50 - 10 = 40\) (км/ч) - скорость от озера до села.

3) \(\frac{60}{40} = \frac{3}{2} = 1,5\) (ч).

Ответ: мотоциклист ехал от озера до села 1,5 ч.

Пояснения:

Решаем задачу с помощью уравнения.

Вводим переменную \(x\) и согласно условию составляем рациональное уравнение, учитывая то, что время рассчитывается по формуле \(t = \frac{S}{v}\), где \(S\) - пройденный путь, \(v\) - скорость движения.

Чтобы избавиться от дробей, умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение, и получаем полное квадратное уравнение, которое решаем через дискриминант. Отрицательный корень отбрасываем, так как скорость не может быть отрицательным числом. Положительный корень соответствует скорости движения от села до города. Далее находим скорость от озера до села и время.