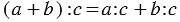Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью  , т.е. 2 : 3 =
, т.е. 2 : 3 =  .
.
Зная дроби, всегда можно разделить одно натуральное число на другое. При этом частное двух натуральных чисел равно дроби, числитель которой - делимое, а знаменатель - делитель. Если обозначить делимое и делитель буквами 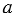 и и 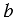 , то , то 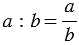 . . |
Пример:
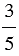 = 3 : 5;
= 3 : 5; 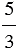 = 5 : 3.
= 5 : 3.
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 = 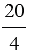 = 5; 13 : 25 =
= 5; 13 : 25 = 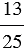 ; 45 : 4 =
; 45 : 4 = 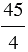 .
.
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
а) 1 = 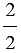 =
= 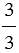 = ... =
= ... = 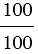 = ..., т.к.
= ..., т.к. 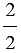 = 2 : 2 = 1,
= 2 : 2 = 1, 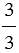 = 3 : 3 = 1, ...,
= 3 : 3 = 1, ..., 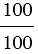 = 100 : 100 = 1, ....
= 100 : 100 = 1, ....
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 = 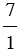 =
= 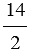 =
= 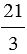 = ..., т.к.
= ..., т.к. 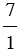 = 7 : 1 = 7,
= 7 : 1 = 7, 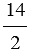 = 14 : 2 = 7;
= 14 : 2 = 7; 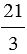 = 21 : 3 = 7 ....
= 21 : 3 = 7 ....
Свойство деления суммы на число
|
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
|
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 - 1,1) : (7,3 + 2,7) можно записать в виде 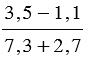 . А выполнив действия в числителе и в знаменателе полученной дроби, найдем значение данного выражения:
. А выполнив действия в числителе и в знаменателе полученной дроби, найдем значение данного выражения: 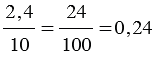 .
.
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
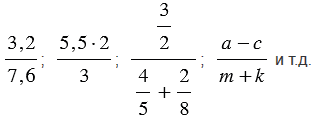
Числитель дробного выражения - выражение, стоящее над чертой.
Знаменатель дробного выражения - выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
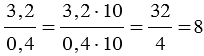 , обычно запись упрощают, и пишут так:
, обычно запись упрощают, и пишут так: 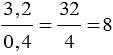 .
.
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
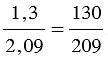 .
.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 1125, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1585, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5.236, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание стр. 57, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.420, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.457, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 13, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.435, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.475, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 2, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 600, Мерзляк, Полонский, Якир, Учебник
Номер 1148, Мерзляк, Полонский, Якир, Учебник
Задание 696, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1148, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1204, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.370, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.416, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.574, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.90, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.32, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 886, Мерзляк, Полонский, Якир, Учебник
Номер 1061, Мерзляк, Полонский, Якир, Учебник
Номер 1177, Мерзляк, Полонский, Якир, Учебник
Номер 1225, Мерзляк, Полонский, Якир, Учебник
Номер 1230, Мерзляк, Полонский, Якир, Учебник
Упражнение 255, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 310, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 919, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 949, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1205, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 266, Мерзляк, Полонский, Якир, Учебник
Номер 362, Мерзляк, Полонский, Якир, Учебник
Упражнение 15, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 258, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 707, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 757, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 859, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 940, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1039, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 809, Макарычев, Миндюк, Учебник
9 класс