Основное свойство дроби
Разделим круг на 4 равные части и закрасим 3 такие части, тогда закрашенная часть составит 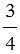 круга.
круга.

Теперь разделим каждую четверть круга на 2 равные части, получим, что круг будет разделен на 8 равных частей и 6 из них будут закрашены, т.е. закрашенная часть составит 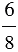 круга.
круга.
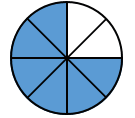
В обоих случаях закрашена одна и та же часть круга, значит, дроби 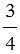 и
и 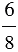 обозначают одну и ту же величину, в таком случае говорят, что
обозначают одну и ту же величину, в таком случае говорят, что 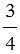 и
и 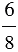 равные дроби и записывают
равные дроби и записывают 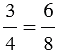 .
.
Если и дальше делить каждую четверть круга на одинаковые доли, то будем получать новые дроби, равные 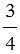 . Так, если разделить каждую четверть на 3, 4, 5 и т.д. равных частей, то всего в круге будет соответственно 4
. Так, если разделить каждую четверть на 3, 4, 5 и т.д. равных частей, то всего в круге будет соответственно 4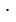 3 = 12 частей, 4
3 = 12 частей, 4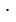 4 = 16 частей, 4
4 = 16 частей, 4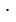 5 = 20 частей и т.д.. А закрашенными из них окажутся соответственно 3
5 = 20 частей и т.д.. А закрашенными из них окажутся соответственно 3 3 = 9 частей, 3
3 = 9 частей, 3 4 = 12 частей, 3
4 = 12 частей, 3 5 = 15 частей и т.д. значит, закрашенная часть круга соответственно выразится дробями
5 = 15 частей и т.д. значит, закрашенная часть круга соответственно выразится дробями 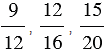 и т.д., значит,
и т.д., значит, 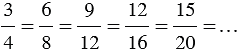 или можно записать так:
или можно записать так: 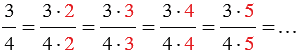 . Полученные равенства показывают, что умножив числитель и знаменатель дроби
. Полученные равенства показывают, что умножив числитель и знаменатель дроби 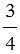 на одно и то же натуральное число, мы получим дробь, равную
на одно и то же натуральное число, мы получим дробь, равную 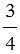 . Также эти равенства можно записать так:
. Также эти равенства можно записать так: 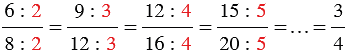 .
.
Основное свойство дроби:
| Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь равная данной. |
Сокращение дробей
| Сокращение дроби - это деление числителя и знаменателя данной дроби на их общий делитель, отличный от 1. |
Пример:
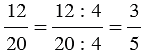
Для удобства сокращение записывают так: 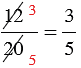 . Числа 3 и 5 - это частные от деления на общий делитель (в данном случае 4) числителя и знаменателя соответственно.
. Числа 3 и 5 - это частные от деления на общий делитель (в данном случае 4) числителя и знаменателя соответственно.
Дробь 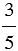 нельзя сократить, т.к. ее числитель и знаменатель не имеют общих делителей, кроме 1, т.е. числитель 3 и знаменатель 5 взаимно простые числа, такую дробь называют несократимой.
нельзя сократить, т.к. ее числитель и знаменатель не имеют общих делителей, кроме 1, т.е. числитель 3 и знаменатель 5 взаимно простые числа, такую дробь называют несократимой.
| Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получится несократимая дробь. |
Пример:
Сократите дробь 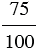 .
.
НОД(75; 100) = 25, тогда 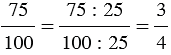 или
или 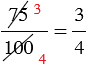 .
.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 5.316, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.338, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.388, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.407, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 9, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание стр. 81, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.89, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.565, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 7.40, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 7.43, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 1126, Мерзляк, Полонский, Якир, Учебник
Задание 488, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 619, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 636, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 875, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.245, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.415, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.472, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.77, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.145, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 52, Мерзляк, Полонский, Якир, Учебник
Номер 574, Мерзляк, Полонский, Якир, Учебник
Номер 678, Мерзляк, Полонский, Якир, Учебник
Номер 1047, Мерзляк, Полонский, Якир, Учебник
Номер 1186, Мерзляк, Полонский, Якир, Учебник
Номер 1224, Мерзляк, Полонский, Якир, Учебник
Упражнение 33, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 86, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 217, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 278, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 542, Мерзляк, Полонский, Якир, Учебник
Номер 647, Мерзляк, Полонский, Якир, Учебник
Номер 648, Мерзляк, Полонский, Якир, Учебник
Номер 900, Мерзляк, Полонский, Якир, Учебник
Номер 911, Мерзляк, Полонский, Якир, Учебник
Упражнение 413, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 533, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 814, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 963, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1011, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс