Квадратные корни. Арифметический квадратный корень
Пусть нам дан квадрат, площадь которого равна 81 квадратная единица. Чему равна длина стороны этого квадрата?
Примем за сторону (в единичных отрезках) квадрата переменную 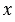 . Тогда площадь квадрата будет равна
. Тогда площадь квадрата будет равна 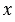 2, а по условию его площадь равна 81 кв. ед. Значит, математическая модель задачи о нахождении стороны квадрата, площадь которого равна 81 кв. ед., может быть представлена в виде уравнения
2, а по условию его площадь равна 81 кв. ед. Значит, математическая модель задачи о нахождении стороны квадрата, площадь которого равна 81 кв. ед., может быть представлена в виде уравнения 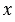 2=81. Корнями данного уравнения являются числа 9 и
2=81. Корнями данного уравнения являются числа 9 и  9. Действительно, 92=81, (
9. Действительно, 92=81, (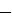 9)2=81. Говорят, что числа 9 и
9)2=81. Говорят, что числа 9 и 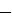 9 являются квадратными корнями из числа 81.
9 являются квадратными корнями из числа 81.
Квадратным корнем из числа  называют число, квадрат которого равен называют число, квадрат которого равен  . . |
Примеры:
Квадратными корнями из числа 36 являются числа 6 и 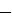 6. Действительно, 62=36, (
6. Действительно, 62=36, (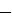 6)2=36.
6)2=36.
Квадратными корнями из числа 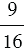 являются числа
являются числа 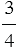 и
и 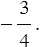 Действительно,
Действительно, 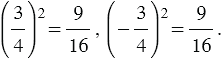
Квадратным корнем из числа 0 является только число 0, так как существует лишь одно число, квадрат которого равен нулю, - это число 0.
Заметим, что не существует числа, квадрат которого равен отрицательному числу, поэтому квадратного корня из отрицательного числа не существует.
Ответом к задаче о нахождении длины стороны квадрата, площадь которого равна 81, является положительный корень уравнения 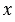 2=81, то есть число 9. Это число называют арифметическим квадратным корнем из числа 81.
2=81, то есть число 9. Это число называют арифметическим квадратным корнем из числа 81.
Арифметическим квадратным корнем из числа  называют неотрицательное число, квадрат которого равен называют неотрицательное число, квадрат которого равен  . . |
Арифметический квадратный корень из числа  обозначают
обозначают 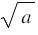 . При этом знак
. При этом знак 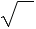 называют знаком арифметического квадратного корня или радикалом (от лат. radix - "корень"). Запись
называют знаком арифметического квадратного корня или радикалом (от лат. radix - "корень"). Запись 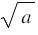 читают: "квадратный корень из
читают: "квадратный корень из  ", опуская при чтении слово "арифметический". Выражение, которое стоит под знаком корня, называют подкоренным выражением. Например, в записи
", опуская при чтении слово "арифметический". Выражение, которое стоит под знаком корня, называют подкоренным выражением. Например, в записи 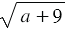 двучлен
двучлен 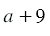 является подкоренным выражением.
является подкоренным выражением.
Заметим, что:

Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня.
Заметим, что к понятию квадратного корня мы пришли, решая уравнение вида 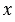 2=
2=  , где
, где 
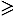 0. Корни этого уравнения - числа, каждое из которых является квадратным корнем из числа
0. Корни этого уравнения - числа, каждое из которых является квадратным корнем из числа  .
.
Графиком функции 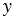 =
= 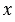 2, является парабола, которая проходит через начало координат и находится выше оси абсцисс. Графиком функции
2, является парабола, которая проходит через начало координат и находится выше оси абсцисс. Графиком функции 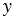 =
=  является прямая параллельная оси абсцисс. Чтобы решить графически уравнение
является прямая параллельная оси абсцисс. Чтобы решить графически уравнение 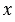 2=
2=  , необходимо на одной координатной плоскости начертить графики данных функций.
, необходимо на одной координатной плоскости начертить графики данных функций.
Уравнение 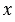 2=
2=  при
при  <0 не имеет корней, так как графики функций
<0 не имеет корней, так как графики функций 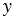 =
= 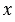 2 и
2 и 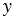 =
=  при
при  <0 общих точек не имеют.
<0 общих точек не имеют.
Уравнение 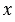 2=
2=  при
при  =0 имеет единственный корень
=0 имеет единственный корень 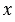 =0, так как графики функций
=0, так как графики функций 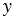 =
= 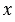 2 и
2 и 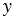 = 0 имеют только одну общую точку.
= 0 имеют только одну общую точку.
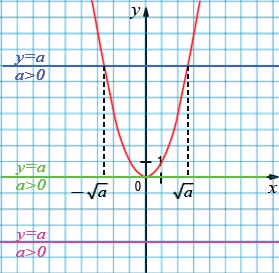
Уравнение 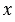 2=
2=  при
при  >0 имеет два корня, так как графики функций
>0 имеет два корня, так как графики функций 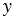 =
= 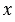 2 и
2 и 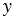 =
= , где
, где  >0, имеют две общие точки. При этом корнями уравнения
>0, имеют две общие точки. При этом корнями уравнения 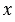 2=
2=  являются числа
являются числа 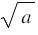 и
и 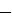
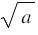 . Действительно,
. Действительно, 
Советуем посмотреть:
Свойства арифметического квадратного корня
Тождественные преобразования выражений, содержащих арифметические квадратные корни
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 744, Мерзляк, Полонский, Якир, Учебник
Номер 795, Мерзляк, Полонский, Якир, Учебник
Номер 892, Мерзляк, Полонский, Якир, Учебник
Упражнение 596, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 655, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 717, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 750, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1330, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс