Упражнение 254 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 86

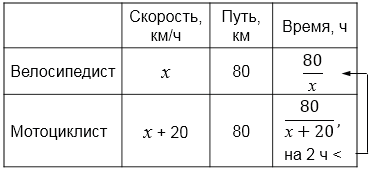
Составим уравнение:

\( \frac{80}{x} - \frac{80}{x+20} = 2\)   \(/\times x(x+20)\)

ОДЗ: \(x \ne 0\)  и  \(x + 20 \ne 0\)

                          \(x \ne -20\)

\( 80(x+20) - 80x = 2x(x+20)\)

\(\cancel{80x} + 1600 - \cancel{80x} = 2x^2 + 40x\)

\(2x^2 + 40x - 1600 = 0\)     \(/ : 2\)

\(x^2 + 20x - 800 = 0\)

\(a = 1\),  \(b = 20\),  \(c = -80\)

\( D = b^2 - 4ac =\)

\(=20^{2} - 4 \cdot 1 \cdot (-800) =\)

\(=400 + 3200 = 3600 > 0\) - 2 корня.

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\),     \( \sqrt{D} = 60. \)

\(x_{1} = \frac{-20 + 60}{2\cdot 1}=\frac{40}{2}=20.\)

\(x_{1} = \frac{-20 - 60}{2\cdot 1}=\frac{-80}{2}=-40\) - не удовлетворяет условию.

Ответ: скорость велосипедиста равна \(20\) км/ч.

Пояснения:

Решаем задачу с помощью уравнения.

Вводим переменную \(x\) и согласно условию составляем рациональное уравнение, учитывая то, что время рассчитывается по формуле \(t = \frac{S}{v}\), где \(S\) - пройденный путь, \(v\) - скорость движения.

Чтобы избавиться от дробей, умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение, и получаем полное квадратное уравнение, которое решаем через дискриминант. Отрицательный корень отбрасываем, так как скорость не может быть отрицательным числом.