Квадратные уравнения. Решение неполных квадратных уравнений.
Ранее мы научились решать линейные уравнения, то есть уравнения вида 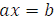 , где
, где 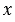 - переменная,
- переменная, 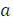 и
и 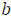 - некоторые числа. Если
- некоторые числа. Если 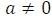 , то данное уравнение называют уравнением первой степени. Числа
, то данное уравнение называют уравнением первой степени. Числа 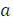 и
и 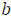 называют коэффициентами уравнения первой степени
называют коэффициентами уравнения первой степени 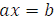 . В данной статье мы поговорим о квадратных уравнениях.
. В данной статье мы поговорим о квадратных уравнениях.
Определение
Квадратным уравнением называют уравнение вида 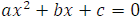 , где , где 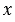 - переменная, - переменная, 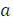 , , 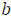 , , 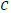 - некоторые числа, причём - некоторые числа, причём 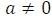 . . |
Числа 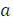 ,
, 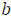 и
и 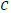 называют коэффициентами квадратного уравнения. Число
называют коэффициентами квадратного уравнения. Число 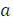 называют первым или старшим коэффициентом, число
называют первым или старшим коэффициентом, число 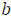 - вторым коэффициентом, число
- вторым коэффициентом, число 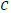 - свободным членом.
- свободным членом.
Квадратное уравнение, первый коэффициент которого равен 1, называют приведённым.
Так как в квадратном уравнении 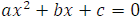 старший коэффициент не равен нулю, то неприведённое квадратное уравнение всегда можно преобразовать в приведённое, имеющее те же корни, для этого обе части данного уравнения надо разделить на число
старший коэффициент не равен нулю, то неприведённое квадратное уравнение всегда можно преобразовать в приведённое, имеющее те же корни, для этого обе части данного уравнения надо разделить на число 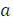 , при этом получим приведённое уравнение
, при этом получим приведённое уравнение 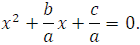
Если в квадратном уравнении 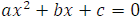 хотя бы один из коэффициентов
хотя бы один из коэффициентов 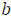 или
или 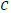 равен нулю, то такое уравнение называют неполным квадратным уравнением.
равен нулю, то такое уравнение называют неполным квадратным уравнением.
Виды неполных квадратных уравнений:
1) при 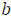 =
= 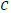 = 0 имеем:
= 0 имеем: 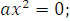
2) при 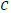 = 0 и
= 0 и 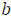
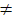 0 имеем:
0 имеем: 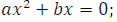
3) при 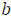 = 0 и
= 0 и 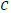
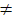 0 имеем:
0 имеем: 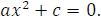
Решим данные уравнения:
1) Поскольку 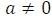 , то уравнение
, то уравнение 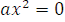 имеет единственный корень
имеет единственный корень 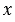 =0.
=0.
2) Уравнение 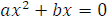 можно представить в следующем виде, вынеся общий множитель за скобку,
можно представить в следующем виде, вынеся общий множитель за скобку, 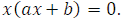 Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, поэтому данное уравнение будет иметь два корня
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, поэтому данное уравнение будет иметь два корня 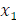 и
и 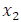 , один из которых равен нулю, а чтобы найти второй корень, необходимо решить уравнение первой степени
, один из которых равен нулю, а чтобы найти второй корень, необходимо решить уравнение первой степени 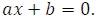 Откуда получаем, что
Откуда получаем, что 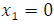 и
и 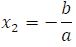 .
.
3) Уравнение 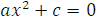 можно представить в виде
можно представить в виде 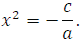 Поскольку
Поскольку 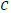
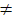 0, то возможны два случая:
0, то возможны два случая: 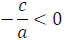 или
или 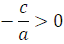 . Очевидно, что в первом случае уравнение корней не имеет, так как не существует числа, квадрат которого отрицательное число. Во втором случае уравнение имеет два корня:
. Очевидно, что в первом случае уравнение корней не имеет, так как не существует числа, квадрат которого отрицательное число. Во втором случае уравнение имеет два корня: 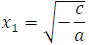 и
и 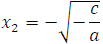 .
.
Советуем посмотреть:
Формула корней квадратного уравнения
Решение уравнений, сводящихся к квадратным уравнениям
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Задание 1066, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 622, Мерзляк, Полонский, Якир, Учебник
Номер 645, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 722, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 780, Мерзляк, Полонский, Якир, Учебник
Номер 824, Мерзляк, Полонский, Якир, Учебник
Номер 931, Мерзляк, Полонский, Якир, Учебник
Упражнение 514, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс