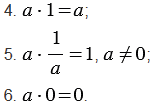Свойства действий с рациональными числами
Свойства сложения рациональных чисел
|
Для любых рациональных чисел
|
Из приведенных свойств сложения чисел следует, что в сумме нескольких рациональных чисел слагаемые можно менять местами и расставлять скобки, тем самым определяя наиболее удобный порядок выполнения действий.
Примеры:
1)  9 + 4 =
9 + 4 =  (9
(9  4) =
4) =  4 и 4 + (
4 и 4 + ( 9) =
9) =  (9
(9  4) =
4) =  5;
5;
 2 + (
2 + ( 6) =
6) =  (2 + 6) =
(2 + 6) =  8 и
8 и  6 + (
6 + ( 2) =
2) =  (6 + 2) =
(6 + 2) =  8;
8;
2) ( 5 + 2,5) + 1,5 =
5 + 2,5) + 1,5 =  (5
(5  2,5) + 1,5 =
2,5) + 1,5 =  2,5 + 1,5 =
2,5 + 1,5 =  (2,5
(2,5  1,5) =
1,5) =  1 и
1 и  5 + (2,5 + 1,5) =
5 + (2,5 + 1,5) =  5 + 4 =
5 + 4 =  (5
(5  4) =
4) =  1;
1;
3)  3 + 0 =
3 + 0 =  3.
3.
Свойства умножения рациональных чисел
|
Для любых рациональных чисел
|
Примеры:
1) ( 2)
2)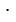 3 =
3 =  (2
(2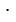 3) =
3) =  6 и 3
6 и 3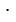 (
( 2) =
2) =  6;
6;
( 5)
5)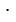 (
( 2) = 10 и (
2) = 10 и ( 2)
2)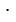 (
( 5) = 10;
5) = 10;
2) ( 2
2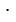 3)
3)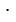 4 =
4 =  6
6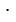 4 =
4 =  24 и
24 и  2
2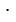 (3
(3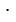 4) =
4) =  2
2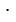 12 =
12 =  24;
24;
3)  5(3
5(3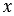 + 2
+ 2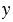 ) =
) =  5
5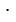 3
3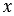 + (
+ ( 5)
5)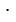 2
2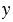 =
=  15
15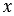 + (
+ ( 10
10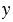 ) =
) =  15
15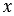
 10
10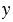 ;
;
4)  4
4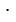 1 =
1 =  4;
4;
5) 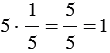 ;
;
6)  7
7 0 = 0.
0 = 0.
Из приведенных свойств умножения следует, что в произведении нескольких рациональных чисел множители можно менять местами, расставлять и раскрывать скобки, тем самым определяя наиболее удобный порядок выполнения действий.
Коэффициент
| Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом или просто коэффициентом. |
Примеры:
1) В выражении 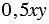 коэффициентом является число 0,5.
коэффициентом является число 0,5.
2) В выражении 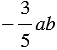 коэффициентом является число
коэффициентом является число 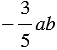 .
.
3) В выражении 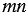 коэффициентом является число 1, т.к.
коэффициентом является число 1, т.к. 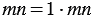 .
.
4) В выражении 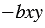 коэффициентом является число
коэффициентом является число  1, т.к.
1, т.к. 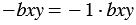 .
.
5) В выражении 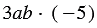 ни одно из чисел 3 и
ни одно из чисел 3 и  5 не является коэффициентом. Но данное выражение можно преобразовать, используя переместительное и сочетательное свойства умножения, получим новое выражение
5 не является коэффициентом. Но данное выражение можно преобразовать, используя переместительное и сочетательное свойства умножения, получим новое выражение 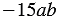 , в котором коэффициентом является число
, в котором коэффициентом является число  15.
15.
Обратите внимание, в выражении 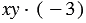 коэффициентом является число
коэффициентом является число  3, но, как правило, коэффициент записывают перед буквенными множителями:
3, но, как правило, коэффициент записывают перед буквенными множителями: 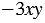 .
.
Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Правило встречается в следующих упражнениях:
6 класс
Номер 979, Мерзляк, Полонский, Якир, Учебник
Номер 1079, Мерзляк, Полонский, Якир, Учебник
Номер 1092, Мерзляк, Полонский, Якир, Учебник
Номер 1103, Мерзляк, Полонский, Якир, Учебник
Номер 1105, Мерзляк, Полонский, Якир, Учебник
Задание 1201, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 4.379, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.44, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.59, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 90, Мерзляк, Полонский, Якир, Учебник
Номер 115, Мерзляк, Полонский, Якир, Учебник
Номер 351, Мерзляк, Полонский, Якир, Учебник
Номер 377, Мерзляк, Полонский, Якир, Учебник
Номер 514, Мерзляк, Полонский, Якир, Учебник
Номер 1202, Мерзляк, Полонский, Якир, Учебник
Упражнение 92, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 735, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 785, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1212, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 41, Мерзляк, Полонский, Якир, Учебник
Номер 188, Мерзляк, Полонский, Якир, Учебник
Номер 206, Мерзляк, Полонский, Якир, Учебник
Номер 285, Мерзляк, Полонский, Якир, Учебник
Упражнение 469, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 515, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 800, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1015, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1020, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1303, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс
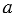 ,
, 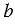 и
и 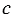 справедливы равенства:
справедливы равенства: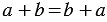 - переместительное свойство сложения;
- переместительное свойство сложения;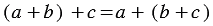 - сочетательное свойство сложения;
- сочетательное свойство сложения;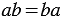 - переместительное свойство умножения;
- переместительное свойство умножения;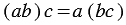 - сочетательное свойство умножения;
- сочетательное свойство умножения;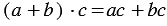 - распределительное свойство умножения относительно сложения;
- распределительное свойство умножения относительно сложения;