Вычитание рациональных чисел
Разностью рациональных чисел 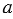 и и 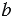 называют такое рациональное число называют такое рациональное число 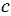 , которое в сумме с числом , которое в сумме с числом 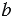 даёт число даёт число 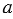 . . |
Например:
12 18 =
18 =  6, так как
6, так как  6 + 18 = 12;
6 + 18 = 12;
25 (
( 8) = 33, так как 33 +(
8) = 33, так как 33 +( 8) = 25;
8) = 25;
 43
43 13 =
13 =  56, так как
56, так как  56 + 13 =
56 + 13 =  43;
43;
 34
34 (
( 15) =
15) =  19, так как
19, так как  19 + (
19 + ( 15) =
15) =  34.
34.
Рассмотрев полученные разности, мы можем заметить, что:
12 18 =
18 =  6, но и 12 + (
6, но и 12 + ( 18) =
18) =  6;
6;
25 (
( 8) = 33, но и 25 + 8 = 33;
8) = 33, но и 25 + 8 = 33;
 43
43 13 =
13 =  56, но и
56, но и  43 + (
43 + ( 13) =
13) =  56;
56;
 34
34 (
( 15) =
15) =  19, но и
19, но и  34 + 15 =
34 + 15 =  19.
19.
То есть вычитание рациональных чисел можно заменить сложением:
|
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:
|
При этом любое выражение, в котором содержатся только знаки сложения и вычитания, можно рассматривать как сумму.
Например:
17 2,5 + 3,7
2,5 + 3,7 46 + 115
46 + 115
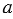 = 17 + (
= 17 + ( 2,5) + 3,7 + (
2,5) + 3,7 + ( 46) + 115 + (
46) + 115 + (
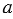 ).
).
Если уменьшаемое больше вычитаемого, то разность положительна:
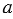

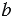
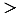 0, если
0, если 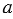
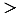
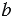 .
.
Если уменьшаемое меньше вычитаемого, то разность отрицательна:
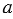

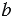
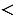 0, если
0, если 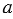
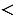
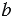 .
.
Если уменьшаемое равно вычитаемому, то разность равна нулю:
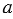

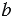 = 0, если
= 0, если 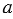 =
= 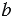 .
.
Мы знаем, что если на координатной прямой заданы, например, две точки А(-12) и В(5), то длина отрезка АВ покажет на сколько единичных отрезков необходимо переместить вправо точку А, чтобы она перешла в точку В. Или другими словами сколько надо прибавить к числу -12, чтобы получить число 5. Пусть АВ = 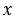 , тогда запишем -12 +
, тогда запишем -12 + 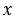 = 5, найдем неизвестное слагаемое и получим, что
= 5, найдем неизвестное слагаемое и получим, что 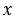 = 5 - (-12) или
= 5 - (-12) или 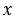 = 17. То есть мы получили, что АВ = 17 единичных отрезков. Из данного примера мы можем сделать вывод:
= 17. То есть мы получили, что АВ = 17 единичных отрезков. Из данного примера мы можем сделать вывод:
| Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. |
Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Свойства действий с рациональными числами
Правило встречается в следующих упражнениях:
6 класс
Номер 1004, Мерзляк, Полонский, Якир, Учебник
Номер 1146, Мерзляк, Полонский, Якир, Учебник
Номер 1152, Мерзляк, Полонский, Якир, Учебник
Задание 1328, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1331, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 4.256, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.278, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.87, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.41, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 403, Мерзляк, Полонский, Якир, Учебник
Номер 410, Мерзляк, Полонский, Якир, Учебник
Номер 638, Мерзляк, Полонский, Якир, Учебник
Номер 651, Мерзляк, Полонский, Якир, Учебник
Номер 994, Мерзляк, Полонский, Якир, Учебник
Номер 1089, Мерзляк, Полонский, Якир, Учебник
Упражнение 608, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 650, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 722, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 886, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 128, Мерзляк, Полонский, Якир, Учебник
Номер 129, Мерзляк, Полонский, Якир, Учебник
Номер 191, Мерзляк, Полонский, Якир, Учебник
Номер 398, Мерзляк, Полонский, Якир, Учебник
Номер 789, Мерзляк, Полонский, Якир, Учебник
Номер 792, Мерзляк, Полонский, Якир, Учебник
Упражнение 593, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 950, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1081, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс