Десятичная запись дробных чисел
Среди обыкновенных дробей выделяют дроби, у которых в знаменателе стоит единица с нулями, т.е. 10, 100, 1 000 и т.д., для таких дробей существует специальная форма записи, в которой используют запятую, например, вместо 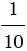 пишут 0,1 (читают: ноль целых одна десятая),
пишут 0,1 (читают: ноль целых одна десятая), 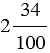 пишут 2,34 (читают: две целых тридцать четыре сотых),
пишут 2,34 (читают: две целых тридцать четыре сотых), 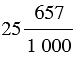 пишут 25,657 (читают: двадцать пять целых шестьсот пятьдесят семь тысячных). Такую форму записи дробей называют десятичной, а саму дробь - десятичной дробью. Запятая отделяет целую часть от дробной.
пишут 25,657 (читают: двадцать пять целых шестьсот пятьдесят семь тысячных). Такую форму записи дробей называют десятичной, а саму дробь - десятичной дробью. Запятая отделяет целую часть от дробной.
Обратите внимание: после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби.
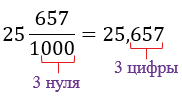
Поэтому вместо 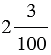 пишут 2,03 (читают: две целых три сотых), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем ноль, чтобы после запятой было два знака, т.к. в знаменателе стоит два нуля, а вместо
пишут 2,03 (читают: две целых три сотых), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем ноль, чтобы после запятой было два знака, т.к. в знаменателе стоит два нуля, а вместо 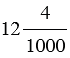 пишут 12,004 (читают: двенадцать целых 4 тысячных), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем два нуля, чтобы после запятой было три знака, т.к. в знаменателе стоит три нуля.
пишут 12,004 (читают: двенадцать целых 4 тысячных), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем два нуля, чтобы после запятой было три знака, т.к. в знаменателе стоит три нуля.
Разряды десятичных дробей
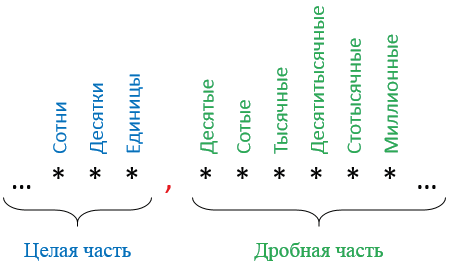
Разрядные единицы:
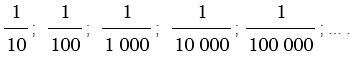
записываются так:
0,1; 0,01; 0,001; 0,0001; 0,00001; ... .
| При чтении десятичной дроби сначала называют ее часть, стоящую перед запятой, и добавляют слово "целых"; затем называют часть, стоящую после запятой, и добавляют название последнего разряда. |
Например, в десятичной дроби 8,4567 последний разряд - это десятитысячные. Поэтому читают ее так: 8 целых 4567 десятитысячных.
|
Чтобы несократимую дробь |
Примеры:
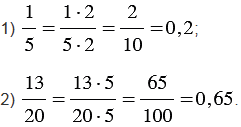
|
Несократимую дробь |
Примеры:
1) 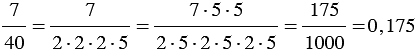 ;
;
2) 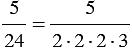 - нельзя преобразовать в десятичную дробь (в разложении знаменателя на простые множители есть 3).
- нельзя преобразовать в десятичную дробь (в разложении знаменателя на простые множители есть 3).
| Чтобы преобразовать обыкновенную дробь в десятичную, можно ее числитель разделить на знаменатель. |
Пример:
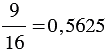
| - | 9 | 0 | 0 | 0 | 0 | 1 | 6 | ||||||
| 8 | 0 | 0 | 5 | 6 | 2 | 5 | |||||||
| - | 1 | 0 | 0 | ||||||||||
| 9 | 6 | ||||||||||||
| - | 4 | 0 | |||||||||||
| 3 | 2 | ||||||||||||
| - | 8 | 0 | |||||||||||
| 8 | 0 | ||||||||||||
| 0 |
Не любую обыкновенную дробь можно записать в виде десятичной дроби. Например, дробь 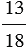 обратить в десятичную нельзя. Разделим числитель данной дроби на знаменатель получим:
обратить в десятичную нельзя. Разделим числитель данной дроби на знаменатель получим:
| - | 1 | 3 | 1 | 8 | ||||||||||
| 1 | 2 | 6 | 0 | , | 7 | 2 | 2 | 2 | . | . | . | |||
| - | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| - | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| - | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| 4 |
Мы видим, что деление можно продолжать бесконечно. И результат деления будет 0,72222... . В данном случае точки означают, что цифра 2 периодически повторяется бесконечно много раз.
Число 0,72222... - это бесконечная периодическая десятичная дробь, или периодическая дробь. Данную дробь принято записывать: 0,7(2) и читать: "нуль целых семь десятых и два в периоде". Цифру (2) называют периодом дроби 0,7(2). Записываем так:
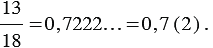
При этом полученную периодическую дробь мы можем округлить до любого из разрядов, например, округлим дробь 0,72222... до десятых, получим:
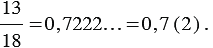
 0,7. В данном случае число 0,7 называют десятичным приближением до десятых дроби
0,7. В данном случае число 0,7 называют десятичным приближением до десятых дроби 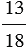 . Запишем:
. Запишем:
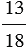
 0,7.
0,7.
|
Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо: 1) выполнить деление до следующего разряда; 2) полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда. |
Советуем посмотреть:
Сложение и вычитание десятичных дробей
Приближенные значения чисел. Округление чисел
Правило встречается в следующих упражнениях:
5 класс
Задание 1267, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1341, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1536, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1636, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 6.188, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.26, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.37, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.92, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 800, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 389, Мерзляк, Полонский, Якир, Учебник
Номер 395, Мерзляк, Полонский, Якир, Учебник
Номер 417, Мерзляк, Полонский, Якир, Учебник
Номер 1098, Мерзляк, Полонский, Якир, Учебник
Номер 1186, Мерзляк, Полонский, Якир, Учебник
Задание 656, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 684, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.245, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.324, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание Проверочная работа, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 80, Мерзляк, Полонский, Якир, Учебник
Номер 138, Мерзляк, Полонский, Якир, Учебник
Номер 254, Мерзляк, Полонский, Якир, Учебник
Номер 426, Мерзляк, Полонский, Якир, Учебник
Номер 637, Мерзляк, Полонский, Якир, Учебник
Упражнение 23, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 103, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 151, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 381, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1015, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 251, Мерзляк, Полонский, Якир, Учебник
Номер 655, Мерзляк, Полонский, Якир, Учебник
Упражнение 484, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 534, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 687, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 793, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 815, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 941, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 981, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1073, Макарычев, Миндюк, Учебник
9 класс
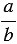 преобразовать в десятичную, необходимо привести ее к одному из знаменателей 10, 100, 1 000 и т.д.
преобразовать в десятичную, необходимо привести ее к одному из знаменателей 10, 100, 1 000 и т.д.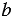 на
на