Уравнения
Уравнение - это равенство, содержащее букву, значение которой надо найти. Например:  + 5 = 10. Чтобы решить данное уравнение, требуется найти такое число, при подстановке которого в данное равенство вместо буквы (то есть найти значение переменной), числовое равенство будет верным. В нашем случае вместо
+ 5 = 10. Чтобы решить данное уравнение, требуется найти такое число, при подстановке которого в данное равенство вместо буквы (то есть найти значение переменной), числовое равенство будет верным. В нашем случае вместо  необходимо подставить 5. Говорят, что число 5 - корень уравнения
необходимо подставить 5. Говорят, что число 5 - корень уравнения  + 5 = 10.
+ 5 = 10.
| Корень уравнения - это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство. |
Корень уравнения - это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение - значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение  + 125 = 200;
+ 125 = 200;
 = 200 - 125;
= 200 - 125;
 = 75.
= 75.
Ответ:  = 75.
= 75.
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение  - 24 = 36;
- 24 = 36;
 = 36 + 24;
= 36 + 24;
 = 60.
= 60.
Ответ:  = 60.
= 60.
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 -  = 115;
= 115;
 = 135 - 115;
= 135 - 115;
 = 20.
= 20.
Ответ:  = 20.
= 20.
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 
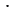 6 = 42;
6 = 42;
 = 42 : 6;
= 42 : 6;
 = 7.
= 7.
Ответ:  = 7.
= 7.
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение  : 12 = 5;
: 12 = 5;
 = 5
= 5 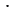 12;
12;
 = 60.
= 60.
Ответ:  = 60.
= 60.
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 :  = 46;
= 46;
 = 184 : 46;
= 184 : 46;
 = 4.
= 4.
Ответ:  = 4.
= 4.
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение  + 36 = 45 и проведем проверку:
+ 36 = 45 и проведем проверку:
 + 36 = 45;
+ 36 = 45;
 = 45 - 36;
= 45 - 36;
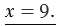
9 + 36 = 45;
45 = 45 - верно.
Ответ:  = 9.
= 9.
Советуем посмотреть:
Степень числа. Квадрат и куб числа
Меньше или больше на сколько? во сколько раз?
Представление числовой информации в таблицах
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 453, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1018, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1073, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1782, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 6.380, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 2.155, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.204, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.281, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 5.520, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 3, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 743, Мерзляк, Полонский, Якир, Учебник
Номер 1205, Мерзляк, Полонский, Якир, Учебник
Задание 223, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 614, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 615, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 790, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 3.122, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.73, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.376, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.79, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 122, Мерзляк, Полонский, Якир, Учебник
Номер 241, Мерзляк, Полонский, Якир, Учебник
Номер 449, Мерзляк, Полонский, Якир, Учебник
Номер 588, Мерзляк, Полонский, Якир, Учебник
Номер 810, Мерзляк, Полонский, Якир, Учебник
Номер 876, Мерзляк, Полонский, Якир, Учебник
Номер 1002, Мерзляк, Полонский, Якир, Учебник
Номер 1235, Мерзляк, Полонский, Якир, Учебник
Упражнение 609, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 659, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 213, Мерзляк, Полонский, Якир, Учебник
Номер 218, Мерзляк, Полонский, Якир, Учебник
Номер 369, Мерзляк, Полонский, Якир, Учебник
Номер 707, Мерзляк, Полонский, Якир, Учебник
Номер 714, Мерзляк, Полонский, Якир, Учебник
Номер 723, Мерзляк, Полонский, Якир, Учебник
Номер 738, Мерзляк, Полонский, Якир, Учебник
Номер 783, Мерзляк, Полонский, Якир, Учебник
Номер 807, Мерзляк, Полонский, Якир, Учебник
Номер 810, Мерзляк, Полонский, Якир, Учебник