Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными

Рассмотрим задачу:

Разность двух чисел равна 4, а их произведение 12. Найдите эти числа.

Решение:

Обозначим первое число буквой , а второе буквой . По условию задачи разность чисел равна 4, т.е. - = 4.

Так как произведение чисел равно 12, то = 12.

Мы составили два уравнения с двумя переменными. Чтобы ответить на вопрос задачи, надо найти такие значения переменных, которые обращают в верное равенство каждое из уравнений - = 4 и = 12, т.е. найти общие решения этих уравнений. В таких случаях говорят, что требуется решить систему уравнений.

Систему уравнений записывают с помощью фигурной скобки. Поэтому, составленную нами систему уравнений, можно записать так:

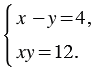
Пара значений переменных = 6, = 2 является решением каждого уравнения системы, т.к. оба равенства 6 - 2 = 4 и 6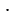2 = 12 являются верными. Такую пару называют решением системы.

Для того чтобы решить систему линейных уравнений с двумя переменными, можно использовать использовать графики уравнений.

Решим систему уравнений:

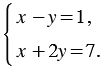
Выразив из уравнения 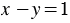переменную через переменную , получим линейную функцию 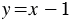. Построим в координатной плоскости график этой функции.

Для этого составим таблицу значений функции для некоторых значений аргумента .

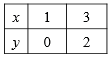
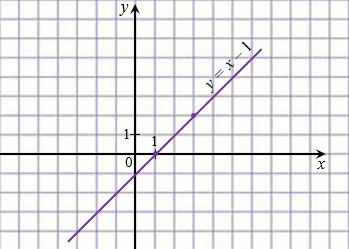
Отметим на координатной плоскости точки с координатами (1; 0) и (3; 2) и проведем через них прямую, которая является графиком линейной функции .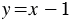

Выразив из уравнения 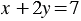переменную через переменную (для этого перенесем переменную из левой части уравнения в правую, изменив ее знак, и разделим обе части уравнения на 2), получим линейную функцию 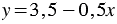. Построим в той же координатной плоскости график этой функции.

Для этого составим таблицу значений функции для некоторых значений аргумента .

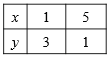
Отметим на имеющейся координатной плоскости точки с координатами (1; 3) и (5; 1) и проведем через них прямую, которая является графиком линейной функции .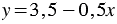

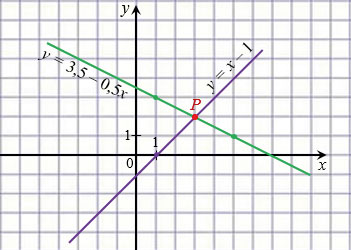
Мы получили, что прямые, которые соответствуют уравнениям 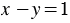и 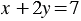, пересекаются в точке Р(3; 2), координаты этой точки удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы. Значит, рассматриваемая система имеет единственное решение: = 3, = 2.

Описанный выше метод решения системы уравнений называют графическим.

Заметим, что графический способ обычно позволяет находить решения лишь приближенно. Поэтому графический метод эффективен в тех случаях, когда требуется определить количество решений системы.

Определим, сколько решений может иметь система двух линейных уравнений с двумя переменными.

1) Если одно из уравнений системы не имеет решения, то и вся система решений не имеет.

2) Если графиком одного из уравнений системы является вся плоскость, то система имеет бесконечно много решений.

3) Если графиками уравнений, входящих в систему линейных уравнений, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.

Рассмотренная нами выше система

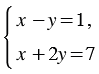
имеет единственное решение  = 3, = 2.

• если прямые совпадают, то система имеет бесконечно много решений.

Рассмотрим систему

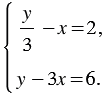
Если умножить обе части первого уравнения этой системы на 3, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:

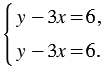
В полученной системе первое и второе уравнения одинаковые, значит, решения этой системы совпадают с решениями уравнения 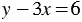. Но это уравнение имеет бесконечно много решений, а следовательно, и рассматриваемая система имеет бесконечно много решений.

• если прямые параллельны, то система решений не имеет.

Рассмотрим систему

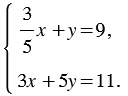
Если умножить обе части первого уравнения этой системы на 5, то решения этого уравнения, а значит, и всей системы не изменятся. Получим:

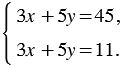
Очевидно, что не существует такой пары значений и , при которых выражение 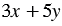одновременно принимает значения и 45, и 11. Следовательно, рассматриваемая система не имеет решений.