Расстояние между параллельными прямыми
Теорема
| Все точки каждой из двух параллельных прямых равноудалены от другой прямой. |
Доказательство:
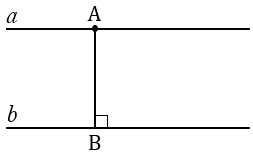
Рассмотрим параллельные прямые  и
и  .
.

Отметим точку А на прямой  и проведем из этой точки перпендикуляр АВ к прямой
и проведем из этой точки перпендикуляр АВ к прямой  .
.
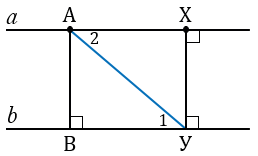
Отметим точку Х на прямой  и докажем, что расстояние от точки Х до прямой
и докажем, что расстояние от точки Х до прямой  равно АВ. Проведем из точки Х перпендикуляр ХУ к прямой
равно АВ. Проведем из точки Х перпендикуляр ХУ к прямой  .
.
ХУ
 , следовательно, ХУ
, следовательно, ХУ
 (т.к. прямая перпендикулярная к одной из параллельных прямых перпендикулярна и ко второй из них).
(т.к. прямая перпендикулярная к одной из параллельных прямых перпендикулярна и ко второй из них).
Рассмотрим 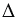 АВУ и
АВУ и 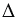 АХУ:
АХУ: 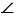 В =
В =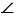 Х = 900, т.е.
Х = 900, т.е. 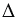 АВУ и
АВУ и 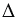 АХУ прямоугольные, АУ - общая гипотенуза,
АХУ прямоугольные, АУ - общая гипотенуза, 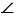 1 =
1 = 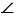 2 (т.к. они накрест лежащие при пересечении параллельных прямых
2 (т.к. они накрест лежащие при пересечении параллельных прямых  и
и  секущей АУ), следовательно,
секущей АУ), следовательно, 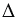 АВУ =
АВУ =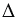 АХУ (по гипотенузе и острому углу), ХУ = АВ.
АХУ (по гипотенузе и острому углу), ХУ = АВ.
Точка Х находится на расстоянии АВ от прямой  , а так как эту точку мы выбрали произвольно, все точки каждой из двух параллельных прямых
, а так как эту точку мы выбрали произвольно, все точки каждой из двух параллельных прямых  и
и  равноудалены от другой прямой. Что и требовалось доказать.
равноудалены от другой прямой. Что и требовалось доказать.
Из доказанной выше теоремы следует, что расстояние между параллельными прямыми - это наименьшее расстояние (перпендикуляр) от каждой точки одной из этих прямых до другой прямой.
Замечание 1
| Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой параллельной данной. |
Доказательство:
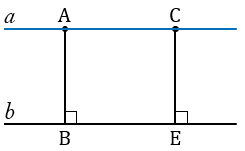
Дано: прямая  , А, С
, А, С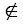
 , АВ
, АВ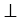
 , СE
, СE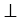
 , АВ = СЕ.
, АВ = СЕ.
Доказать: А, С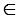
 и
и 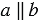 .
.
Доказательство:
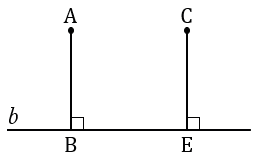
По аксиоме параллельных прямых через точку А проходит единственная прямая параллельная прямой  . Проведем через точку А прямую
. Проведем через точку А прямую  параллельную
параллельную  .
.
По теореме, доказанной выше, все точки, лежащие на прямой  равноудалены от точек прямой
равноудалены от точек прямой  .
.
Предположим, что точка С не лежит на прямой  , тогда расстояние от точки С до прямой
, тогда расстояние от точки С до прямой  будет больше или меньше, чем расстояние АВ.
будет больше или меньше, чем расстояние АВ.
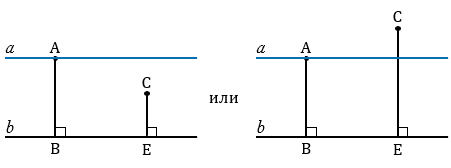
Но по условию АВ = СЕ, следовательно, получили противоречие, значит, наше предположение неверно и А, С
 , при этом по построению
, при этом по построению  . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание 2
| Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной прямой. |
Доказательство:
Пусть  - данная прямая, d - данное расстояние. Отметим на прямой
- данная прямая, d - данное расстояние. Отметим на прямой  произвольную точку А и проведем отрезок АВ длины d так, что АВ
произвольную точку А и проведем отрезок АВ длины d так, что АВ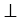
 , через точку В по аксиоме параллельных прямых проходит единственная прямая параллельная прямой
, через точку В по аксиоме параллельных прямых проходит единственная прямая параллельная прямой  . Проведем через точку В прямую
. Проведем через точку В прямую  параллельную
параллельную  .
.
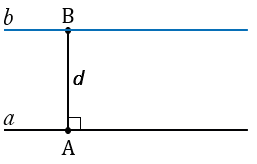
По доказанной выше теореме все точки прямой  находятся на расстоянии d от прямой
находятся на расстоянии d от прямой  , т.е. все эти точки принадлежат искомому множеству. В силу обратной теоремы любая точка искомого множества лежит на прямой
, т.е. все эти точки принадлежат искомому множеству. В силу обратной теоремы любая точка искомого множества лежит на прямой  . Значит, прямая
. Значит, прямая  является геометрическим местом всех точек, удовлетворяющих данному условию. Что и требовалось доказать.
является геометрическим местом всех точек, удовлетворяющих данному условию. Что и требовалось доказать.
Геометрическое место точек, удовлетворяющих данному условию - множество всех точек, удовлетворяющих какому-либо условию.
1) каждая точка данной фигуры должна обладать заданным свойством;
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 278, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 279, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 280, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 283, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 294, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 443, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1095, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник