1. Главная
  2. ГДЗ
  3. 7 класс, 8 класс, 9 класс
  4. Геометрия
  5. Атанасян учебник
  6. 334

Задание 334 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник

Старая и новая редакции

Вернуться к содержанию учебника

331 332 333 334 335 336 337

Выберите год учебника

Вопрос

№334 учебника 2013-2022 (стр. 93):

Через каждую вершину данного треугольника проведена прямая, перпендикулярная к биссектрисе треугольника, исходящей из этой вершины. Отрезки этих прямых вместе со сторонами данного треугольника образуют три треугольника. Докажите, что углы этих треугольников соответственно равны.

№334 учебника 2023-2024 (стр. 95):

Даны угол и отрезок AB. Постройте точку M, равноудалённую от сторон угла и такую, что МА = МВ.

Подсказка

№334 учебника 2013-2022 (стр. 93):

Вспомните:

  1. Какая фигура называется треугольником.
  2. Что такое биссектриса треугольника.
  3. Какие прямые называются перпендикулярными.
  4. Теорему о сумме углов треугольника.

№334 учебника 2023-2024 (стр. 95):

Ответ

331 332 333 334 335 336 337

№334 учебника 2013-2022 (стр. 93):

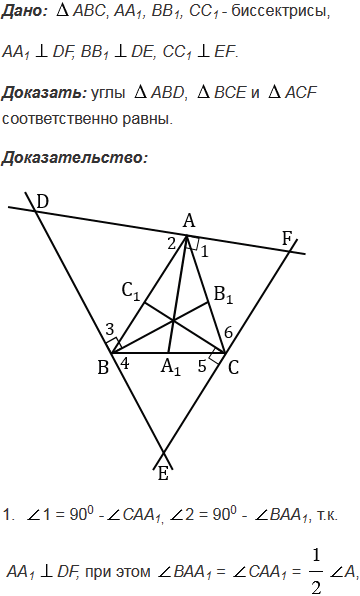
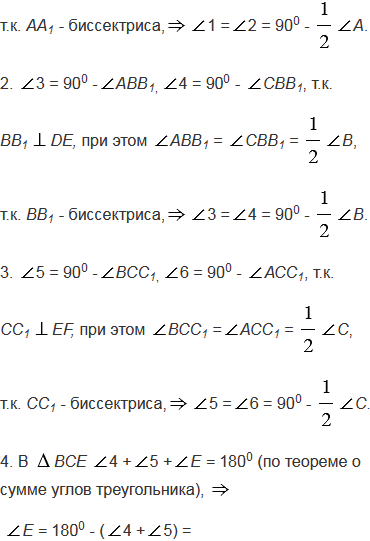
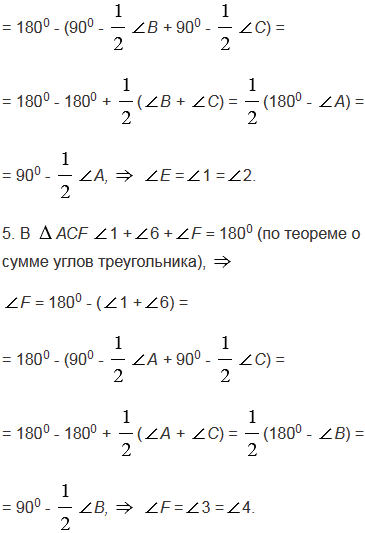
№334 учебника 2023-2024 (стр. 95):

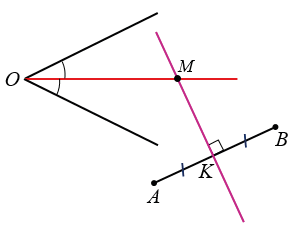
Искомая точка М - точка пересечения биссектрисы данного угла (ОМ) и серединного перпендикуляра к данному отрезку (КМ).

Пояснения:

Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. А каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Следовательно, точкой равноудаленной от сторон угла и равноудаленной от концов отрезка, будет точка пересечения биссектрисы данного угла и серединного перпендикуляра к данному отрезку.

331 332 333 334 335 336 337

Вернуться к содержанию учебника