Задание 412 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№412 учебника 2013-2022 (стр. 112):
Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12 см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е - на гипотенузе треугольника. Найдите периметр квадрата.
№412 учебника 2023-2024 (стр. 115):
Постройте оси симметрии двух пересекающихся прямых
Подсказка
№412 учебника 2013-2022 (стр. 112):
Вспомните:
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
- Какой треугольник называется равнобедренным.
- Свойства равнобедренного треугольника.
- Что такое квадрат.
№412 учебника 2023-2024 (стр. 115):
Вспомните:
- Какие прямые называют пересекающимися.
- Что называют биссектрисой угла.
- Свойство биссектрисы угла.
- Какие углы называют вертикальными.
- Какие фигуры называют симметричными относительно прямой.
- Как построить биссектрису угла.
Ответ
№412 учебника 2013-2022 (стр. 112):
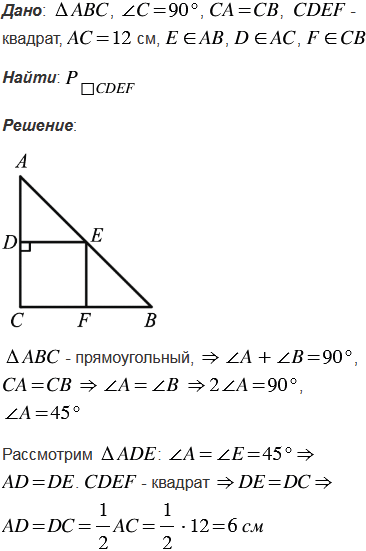


№412 учебника 2023-2024 (стр. 115):
Дано: 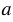
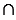 b = О.
b = О.
Построить: оси симметрии и b.
Решение:
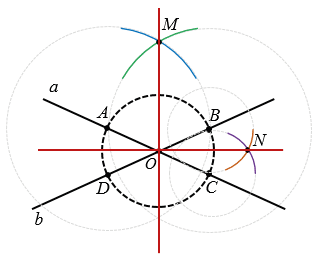
ОМ и ОN - биссектрисы вертикальных углов, полученных при пересечении прямых 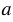 и b,
и b, 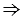 ОМ и ОN - оси симметрии пересекающихся прямых
ОМ и ОN - оси симметрии пересекающихся прямых 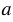 и b.
и b.
Пояснения:
Пусть нам даны две пересекающие прямые 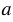 и b, О - их точка пересечения. т.е.
и b, О - их точка пересечения. т.е. 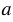
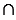 b = О.
b = О.
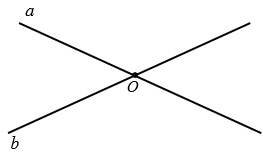
Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Данная прямая называется осью симметрии этих фигур. Две точки А и А1 называются симметричными относительно прямой 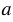 , если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая
, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Прямая 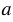 называется осью симметрии точек A и A1. Каждая точка оси
называется осью симметрии точек A и A1. Каждая точка оси 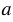 симметрична самой себе.
симметрична самой себе.
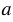 , то они либо параллельны, либо их точка пересечения лежит на оси симметрии
, то они либо параллельны, либо их точка пересечения лежит на оси симметрии 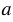 .
. в точках А и С, а прямую b - в точках В и D.
в точках А и С, а прямую b - в точках В и D.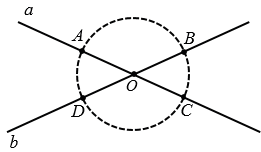
Теперь с помощью циркуля чертим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке в точке М. Через точки О и М проводим биссектрису ОМ вертикальных углов АОВ и СОD.
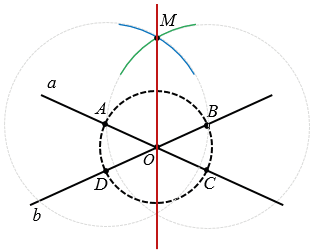
Далее с помощью циркуля чертим две окружности с центрами в точках С и В радиуса ВС (полностью окружности строить необязательно, смотри выделенное фиолетовым и коричневым и зеленым цветом). Эти окружности пересекутся в точке в точке N. Через точки О и N проводим биссектрису ОN вертикальных углов BОC и AОD.

Мы построили биссектрисы ОМ и ОN вертикальных углов, полученных при пересечении двух прямых  и b в точке О, которые являются осями симметрии этих пересекающихся прямых
и b в точке О, которые являются осями симметрии этих пересекающихся прямых 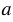 и b, т.к. каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
и b, т.к. каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Вернуться к содержанию учебника