Остроугольный, прямоугольный и тупоугольный треугольники
В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой. Данный вывод можно сделать на основе теоремы о сумме углов треугольника, так как если в треугольнике один из углов тупой или прямой, то сумма других двух не будет превосходить 900, т.е. каждый из них будет являться острым.
- Остроугольный треугольник - это треугольник, у которого все три угла острые.
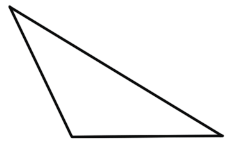
- Тупоугольный треугольник - это треугольник, у которого один из углов тупой.
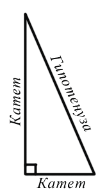
- Прямоугольный треугольник - это треугольник, у которого один из углов прямой. У данного треугольника сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны - катетами.
Советуем посмотреть:
Теорема о сумме углов треугольника
Теорема о соотношениях между сторонами и углами треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 350, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 445, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 530, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 745, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 849, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 886, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1033, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 369, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1334, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 676, Мерзляк, Полонский, Якир, Учебник
Номер 677, Мерзляк, Полонский, Якир, Учебник