Упражнение 259 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 87

Пусть скорость течения равна \(x\) км/ч.

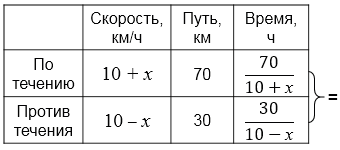
Составим уравнение:

\( \frac{70}{10 + x} = \frac{30}{10 - x}\) \(/\times (10+x)(10-x)\)

ОДЗ: \(10 + x \ne 0\)  и  \(10 - x \ne 0\)

          \(x \ne -10\)          \(x \ne 0\)

\( 70(10 - x) = 30(10 + x) \)

\( 700 - 70x = 300 + 30x \)

\(-70x - 30 x = 300 - 700\)

\(-100x = -400\)

\(x = \frac{-400}{-100}\)

\(x = 4\)

Ответ: скорость течения равна \(4\) км/ч.

Пояснения:

Скорость по течению реки равна сумме собственной скорости и скорости течения реки.

Скорость против течения реки равна разности собственной скорости и скорости течения реки.

Решаем задачу с помощью уравнения.

Вводим переменную \(x\) - скорость течения реки и согласно условию составляем рациональное уравнение, учитывая то, что время рассчитывается по формуле \(t = \frac{S}{v}\), где \(S\) - пройденный путь, \(v\) - скорость движения .

Чтобы избавиться от дробей, умножаем обе части уравнения на общий знаменатель дробей, входящих в уравнение, и получаем линейное уравнение, корень которого соответствует скорости течения реки.