Формула корней квадратного уравнения

В данной статье мы выведем формулу корней квадратного уравнения, которая позволит по коэффициентам , и квадратного уравнения находить его корни. Итак, имеем квадратное уравнение:

Так как , то, умножив обе части этого уравнения на 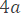получим уравнение, которое будет равносильно данному:

Теперь выделим в левой части полученного уравнения квадрат двучлена:

Теперь существование корней уравнения (2) и их количество зависит от значения выражения . Данное значение называют дискриминантом (от лат. discriminare - "различать", "разделять") квадратного уравнения и обозначают буквой , то есть

То есть уравнение (2) можно записать следующим образом:

Очевидно, что возможны три случая: <0, = 0, >0. Рассмотрим каждый случай отдельно.

1. Если <0, то уравнение (3), а следовательно, и уравнение (1) корней не имеют, так как при любом значении выражение принимает только неотрицательные значения.

Вывод: если <0, то квадратное уравнение корней не имеет.

2. Если = 0, то уравнение(3) принимает вид:

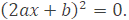
Откуда имеем

Вывод: если = 0, то квадратное уравнение имеет один корень

3. Если >0, то уравнение (3) можно записать в виде

Отсюда или . Тогда или

Вывод: если > 0, то квадратное уравнение имеет два корня и :

Применима и краткая форма записи:

Эту запись называют формулой корней квадратного уравнения

Эту формулу можно применять и в случае, когда = 0. Имеем:

Алгоритм решения квадратных уравнений:

• найти дискриминант квадратного уравнения;
• если < 0, то в ответе записать, что корней нет;
• если 0, то воспользоваться формулой корней квадратного уравнения.

Если второй коэффициент квадратного уравнения представить в виде , то можно пользоваться другой формулой, которая во многих случаях облегчает вычисления. Рассмотрим квадратное уравнение

Найдем его дискриминант:

Обозначим выражение через

Если 0, то по формуле корней квадратного уравнения получаем:

то есть

, где