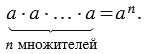Степень числа. Квадрат и куб числа
Определение.
|
Степенью числа "
|
Выражение "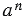 " читают так: "
" читают так: " в степени
в степени 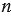 " или "
" или "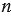 - ая степень числа
- ая степень числа  ", и называют степенью. При этом в этой записи число "
", и называют степенью. При этом в этой записи число " " называют основанием степени, а число "
" называют основанием степени, а число "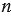 ", которое показывает число множителей в произведении, - показателем степени.
", которое показывает число множителей в произведении, - показателем степени.
Например, найдем значение следующих степеней:
24 = 2 2
2 2
2 2 = 4
2 = 4 2
2 2 = 8
2 = 8 2 = 16;
2 = 16;
36 = 3 3
3 3
3 3
3 3
3 3 = 9
3 = 9 3
3 3
3 3
3 3 = 27
3 = 27 3
3 3
3 3 = 81
3 = 81 3
3 3 =243
3 =243 3 = 729.
3 = 729.
Квадрат числа - это вторая степень числа. Квадрат числа записывают так: 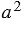 . Читают: "
. Читают: " в квадрате" или "
в квадрате" или " во второй степени".
во второй степени".
Например, найдем квадрат чисел 4 и 8:
42 = 4 4 = 16;
4 = 16;
82 = 8 8 = 64.
8 = 64.
Куб числа - это третья степень числа. Куб числа записывают так: 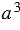 . Читают: "
. Читают: " в кубе" или "
в кубе" или " в третей степени".
в третей степени".
Например, найдем куб чисел 5 и 7:
53 = 5 5
5 5 = 25
5 = 25 5 = 125;
5 = 125;
73 = 7 7
7 7 = 49
7 = 49 5 = 343;
5 = 343;
Степенью числа " " с показателем
" с показателем 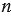 = 1 является само это число, то есть
= 1 является само это число, то есть 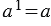 .
.
Ноль в любой степени - это ноль, единица - это единица.
0n = 0;
1n = 1.
Действительно, т.к. степень можно расписать как произведение, то, если в основании находится ноль, то мы получим произведение n нолей, если единица - произведение n единиц.
Возведение числа в степень - это пятое арифметическое действие, поэтому стоит учитывать, что:
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом - остальные действия, в соответствии с порядком их выполнения.
Например, найдем значение выражения 6 42 - (3 + 2):
42 - (3 + 2):
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:
6 42 - (3 + 2) = 6
42 - (3 + 2) = 6 16 - (3 + 2) = 6
16 - (3 + 2) = 6 16 - 5 = 96 - 5 = 91.
16 - 5 = 96 - 5 = 91.
Советуем посмотреть:
Меньше или больше на сколько? во сколько раз?
Представление числовой информации в таблицах
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 660, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 719, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1442, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 660, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание стр. 119, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание В.10, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.161, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 5.557, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 590, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 164, Мерзляк, Полонский, Якир, Учебник
Номер 351, Мерзляк, Полонский, Якир, Учебник
Номер 629, Мерзляк, Полонский, Якир, Учебник
Номер 760, Мерзляк, Полонский, Якир, Учебник
Задание 883, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 888, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.271, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.322, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.114, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.17, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 64, Мерзляк, Полонский, Якир, Учебник
Номер 129, Мерзляк, Полонский, Якир, Учебник
Номер 135, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Упражнение 131, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 221, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 270, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 357, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 408, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 395, Мерзляк, Полонский, Якир, Учебник
Номер 400, Мерзляк, Полонский, Якир, Учебник
Номер 408, Мерзляк, Полонский, Якир, Учебник
Номер 410, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 552, Мерзляк, Полонский, Якир, Учебник
Номер 559, Мерзляк, Полонский, Якир, Учебник
Номер 571, Мерзляк, Полонский, Якир, Учебник
Номер 775, Мерзляк, Полонский, Якир, Учебник
Номер 901, Мерзляк, Полонский, Якир, Учебник
9 класс