Тождественные преобразования выражений, содержащих арифметические квадратные корни
Рассмотрим выражение 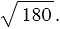
Используя теорему об арифметическом квадратном корне из произведения, получим:
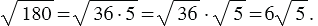 (1)
(1)
Данное выражение мы представили в виде произведения рационального числа 6 и иррационального числа 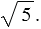 Данное преобразование называют вынесением множителя из-под знака корня, мы вынесли из-под корня множитель 6.
Данное преобразование называют вынесением множителя из-под знака корня, мы вынесли из-под корня множитель 6.
Пример 1: Вынесите множитель из-под знака корня:
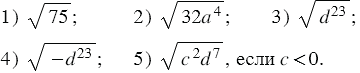
1) Представим подкоренное выражение в виде произведения двух чисел, одно из которых является квадратом рационального числа, тогда мы можем записать:
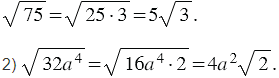
3) Нам известно, что значение подкоренного выражения должно быть неотрицательным, поэтому из условия следует, что 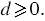 Тогда имеем:
Тогда имеем:
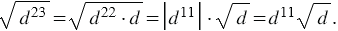
4) Нам известно, что значение подкоренного выражения должно быть неотрицательным, поэтому из условия следует, что 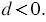 Тогда имеем:
Тогда имеем:
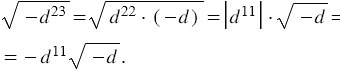
5) Квадрат любого числа есть число неотрицательное, то есть 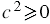 , учитывая это и то, что значение подкоренного выражения должно быть неотрицательным, получаем, что
, учитывая это и то, что значение подкоренного выражения должно быть неотрицательным, получаем, что 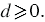 Тогда имеем:
Тогда имеем:
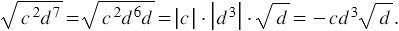
Рассмотрим преобразование (1) в обратном порядке:
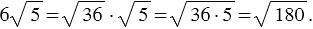 (2)
(2)
Данное преобразование называют внесением множителя под знак корня. Мы внесли под знак корня множитель 6.
Пример 2: Внесите множитель под знак корня:
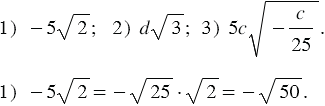
2) Если 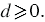 , то
, то 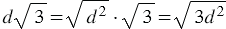 ; если
; если 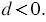 , то
, то 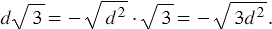
3) Так как значение подкоренного выражения должно быть неотрицательным, то 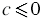 , тогда:
, тогда:
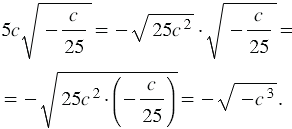
Освободиться от иррациональности в знаменателе дроби означает преобразовать дробь так, чтобы её знаменатель не содержал квадратного корня.
Пример 3: Освободитесь от иррациональности в знаменателе дроби:
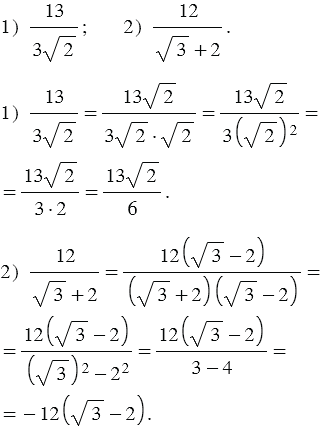
Советуем посмотреть:
Квадратные корни. Арифметический квадратный корень
Свойства арифметического квадратного корня
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 524, Мерзляк, Полонский, Якир, Учебник
Номер 542, Мерзляк, Полонский, Якир, Учебник
Номер 564, Мерзляк, Полонский, Якир, Учебник
Номер 565, Мерзляк, Полонский, Якир, Учебник
Номер 9, Мерзляк, Полонский, Якир, Учебник
Упражнение 403, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 408, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 414, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 428, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 430, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс