Функция y = √x и её график
Пусть нам дан квадрат, площадь которого равна 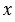 , тогда его сторону, равную
, тогда его сторону, равную 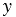 , можно найти по формуле
, можно найти по формуле 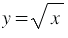 . При этом изменение площади квадрата
. При этом изменение площади квадрата 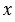 приводит и к изменению его стороны
приводит и к изменению его стороны 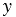 .
.
Зависимость переменной 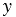 от переменной
от переменной 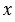 является функциональной, а формула
является функциональной, а формула 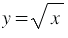 задает функцию, так как каждому значению переменной
задает функцию, так как каждому значению переменной 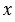 соответствует единственное значение переменной
соответствует единственное значение переменной 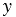 .
.
Областью определения функции 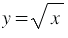 является множество неотрицательных чисел. Областью значений функции
является множество неотрицательных чисел. Областью значений функции 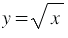 является множество неотрицательных чисел. Очевидно, что если
является множество неотрицательных чисел. Очевидно, что если 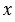 =0, то
=0, то 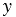 =0 (то есть нуль функции - значение аргумента, при котором значение функции равно 0, - это
=0 (то есть нуль функции - значение аргумента, при котором значение функции равно 0, - это 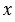 =0). Учитывая это, можно сделать вывод, что график данной функции расположен в первой координатной четверти, при этом начало координат принадлежит графику функции.
=0). Учитывая это, можно сделать вывод, что график данной функции расположен в первой координатной четверти, при этом начало координат принадлежит графику функции.
Составим таблицу значений функции 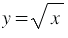 :
:
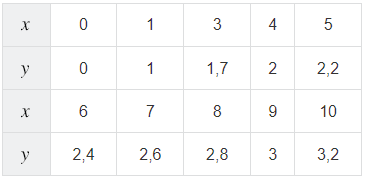
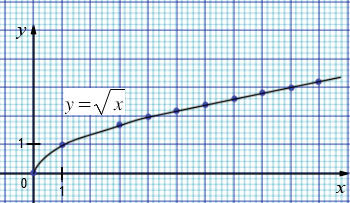
Построим на координатной плоскости точки, координаты которых указаны в таблице, затем проведем от начала координат через эти точки плавную линию, получим график функции 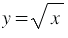 , который является развернутой ветвью параболы.
, который является развернутой ветвью параболы.
Пусть 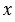 1<
1<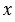 2 - два произвольных значения аргумента функции
2 - два произвольных значения аргумента функции 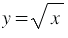 . Тогда из свойства арифметического квадратного корня следует, что
. Тогда из свойства арифметического квадратного корня следует, что 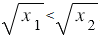 . Это означает, что большему значению аргумента функции
. Это означает, что большему значению аргумента функции 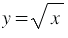 соответствует большее значение функции. Верно и обратное утверждение: большему значению функции соответствует большее значение аргумента, то есть если
соответствует большее значение функции. Верно и обратное утверждение: большему значению функции соответствует большее значение аргумента, то есть если 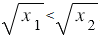 , то
, то 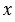 1<
1<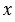 2.
2.
Свойства функции \( y = \sqrt{x} \):
1. Функция определена при любых неотрицательных значениях аргумента, т.е. \(D(y) = [0; +\infty)\).
2. Функция принимает только неотрицательные значения, причем любое неотрицательное число может являться ее значением, т.е. \(E(y) = [0; + \infty)\).
3. Функция обращается в нуль при \(x = 0\).
4. Функция является возрастающей.
Советуем посмотреть:
Квадратные корни. Арифметический квадратный корень
Свойства арифметического квадратного корня
Тождественные преобразования выражений, содержащих арифметические квадратные корни
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 582, Мерзляк, Полонский, Якир, Учебник
Номер 596, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Упражнение 349, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 350, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1128, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1153, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1164, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс