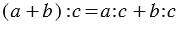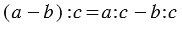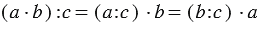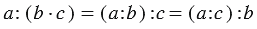Деление натуральных чисел
Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.
Рассмотрим задачу:
У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?
Пусть яблок досталось каждому кролику, тогда мы можем сказать, что общее количество яблок равно: 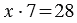 . Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно - это 4: - верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
. Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно - это 4: - верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
| Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением. |
Данное действие записывают так: 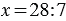 ,
, 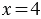 или
или 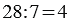 , где:
, где:
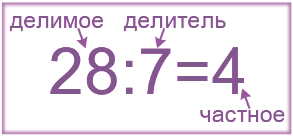
|
Запомните: Делимое - это то число, которое делят. Делитель - это то число, на которое делят. Частное - это результат деления. |
Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос "во сколько?", для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.
Из вышесказанного мы можем сделать вывод:
1. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
Пример: 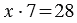 , следовательно,
, следовательно, 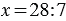 , то есть
, то есть 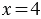 .
.
2. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Пример: 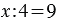 , по смыслу деления
, по смыслу деления 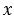 - это произведение 4 и 9, следовательно,
- это произведение 4 и 9, следовательно, 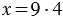 , то есть
, то есть 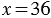 .
.
3. Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Пример: 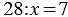 , по смыслу деления число 28 - это произведение множителей
, по смыслу деления число 28 - это произведение множителей 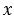 и 7, то есть мы можем записать:
и 7, то есть мы можем записать: 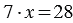 , теперь, применяя пункт 1, получаем:
, теперь, применяя пункт 1, получаем: 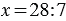 , то есть
, то есть 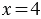 .
.
Свойства деленияРаспределительные свойства: 1. Деление суммы на число: 2. Деление разности на число: 3. Деление произведения на число: 4. Деление числа на произведение: Действия с единицей и нулем 1. Деление числа на единицу: 2. Деление числа на себя: 3. Деление нуля на число: НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ! |
Свойства деления
Распределительные свойства:
1. Деление суммы на число:
У Вани и Маши 3 кролика. Маша нашла 9 яблок, а Ваня - 15. Сколько яблок досталось каждому кролику?
Решение:
а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:
1) 9 + 15 = 24 (я) - собрали Маша и Ваня вместе.
2) 24 : 3 = 8 (я) - досталось каждому кролику.
б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:
1) 9 : 3 = 3 (я) - принесла Маша каждому кролику.
2) 15 : 3 = 5 (я) - принес Ваня каждому кролику.
3) 3 + 5 = 8 (я) - досталось каждому кролику.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.
Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
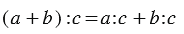
2. Деление разности на число:
Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?
а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:
1) 150 - 72 = 78 (руб.) - осталось после покупки цветов.
2) 78 : 3 = 26 (руб.) - осталось у каждого брата.
б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:
1) 150 : 3 = 50 (руб.) - получил каждый брат.
2) 72 : 3 = 24 (руб.) - потратил каждый брат.
3) 50 - 24 = 26 (руб.) - осталось у каждого брата.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (150 - 72) : 3 = 150 : 3 - 72 : 3.
Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
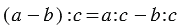
3. Деление произведения на число:
В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?
а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:
1) 12 · 6 = 72 (я) - принесли всего дети.
2) 72 : 3 = 24 (я) - досталось каждому кролику.
б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:
1) 12 : 3 = 4 (чел.) - принесли яблоки 1 кролику.
2) 4 · 6 =24 (я) - досталось каждому кролику.
б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:
1) 6 : 3 = 2 (я) - принес каждый ребенок для одного кролика.
2) 2 · 12 = 24 (я) - досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.
Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
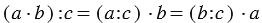
4. Деление числа на произведение:
В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?
а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:
1) 4 · 3 = 12 (к) - всего в клетках.
2) 48 : 12 = 4 (я) - досталось каждому кролику.
б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:
1) 48 : 4 = 12 (я) - положат в каждую клетку.
2) 12 : 3 = 4 (я) - досталось каждому кролику.
Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:
а) 1) 4 · 3 = 12 (к) - всего в клетках.
2) 48 : 12 = 4 (я) - досталось каждому кролику.
б) 1) 48 : 3 = 16 (я) - положат в каждую клетку.
2) 16 : 4 = 4 (я) - досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4
Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.
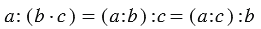
Действия с единицей и нулем
1. Деление числа на единицу:
У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?
Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:
3 : 1 = 3 (я) - достанется кролику, следовательно, мы можем сделать вывод: При делении числа на единицу получается само число: 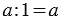
2. Деление числа на себя:
Из свойств умножения мы знаем, что: 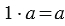 , а мы знаем, что по смыслу деления можно записать, что:
, а мы знаем, что по смыслу деления можно записать, что: 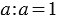 , то есть при делении числа, не равного нулю, на само себя получается единица.
, то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число:
Рассуждая аналогично пункту 2 получаем: 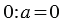 , то есть при делении ноля на любое число, не равное нулю, получаем ноль.
, то есть при делении ноля на любое число, не равное нулю, получаем ноль.
Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Это легко объяснить следующими рассуждениями: пусть мы взяли 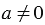 карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по
карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по 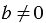 карандашей в каждой коробке:
карандашей в каждой коробке: 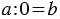 , из смысла деления
, из смысла деления 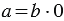 , в то же время мы знаем из свойств умножения, что:
, в то же время мы знаем из свойств умножения, что: 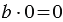 , то есть получаем, что
, то есть получаем, что 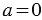 , а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
, а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
Советуем посмотреть:
Степень числа. Квадрат и куб числа
Меньше или больше на сколько? во сколько раз?
Представление числовой информации в таблицах
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 1105, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5.47, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.86, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.387, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 2.226, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.89, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.141, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.177, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 11, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 584, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 68, Мерзляк, Полонский, Якир, Учебник
Номер 113, Мерзляк, Полонский, Якир, Учебник
Номер 196, Мерзляк, Полонский, Якир, Учебник
Номер 208, Мерзляк, Полонский, Якир, Учебник
Задание 83, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1.17, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.51, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.400, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.88, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 12, Мерзляк, Полонский, Якир, Учебник
Номер 63, Мерзляк, Полонский, Якир, Учебник
Номер 328, Мерзляк, Полонский, Якир, Учебник
Номер 820, Мерзляк, Полонский, Якир, Учебник
Номер 849, Мерзляк, Полонский, Якир, Учебник
Номер 1070, Мерзляк, Полонский, Якир, Учебник
Упражнение 65, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 367, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 625, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 265, Мерзляк, Полонский, Якир, Учебник
Номер 701, Мерзляк, Полонский, Якир, Учебник
9 класс