Уравнения с двумя переменными
Равенства, содержащие две переменные, называют уравнениями с двумя переменными. Если при изучении уравнений с одной переменной говорят о их корнях, то, имея уравнение с двумя переменными, говорят о парах чисел - его решениях.
| Пару значений переменных, обращающую уравнение в верное равенство, называют решением уравнения с двумя переменными. |
Факт того, что пара чисел 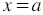 ,
, 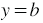 является решением уравнения, условились записывать так:
является решением уравнения, условились записывать так: 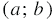 является решением уравнения. При такой записи на первом месте обязательно ставят значение той переменной, которая по алфавиту идет первой, в нашем случае это значение переменной
является решением уравнения. При такой записи на первом месте обязательно ставят значение той переменной, которая по алфавиту идет первой, в нашем случае это значение переменной 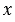 . При этом уравнение с двумя переменными может иметь как бесконечно много решений, так и не иметь не одного.
. При этом уравнение с двумя переменными может иметь как бесконечно много решений, так и не иметь не одного.
| Решить уравнение с двумя переменными - это значит найти все его решения или показать, что оно не имеет решений. |
Свойства уравнений с двумя переменными:
- Если к обеим частям данного уравнения прибавить (или из обеих их частей вычесть) одно и то же число, то получим уравнение, имеющее те же решения, что и данное.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же решения, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же решения, что и данное.
Как говорилось выше решением уравнения с двумя переменными является пара чисел, например 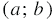 , то мы можем изобразить это решение в виде точки М
, то мы можем изобразить это решение в виде точки М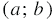 на координатной плоскости. Если мы изобразим все решения уравнения, то получим график уравнения.
на координатной плоскости. Если мы изобразим все решения уравнения, то получим график уравнения.
| Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения. |
Если какая-то фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, - это пара чисел, которая является решением данного уравнения.
Советуем посмотреть:
Линейное уравнение с двумя переменными и его график
Решение систем линейных уравнений методом подстановки
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Линейные неравенства с двумя переменными и их системы
Исследование системы двух линейных уравнений с двумя переменными
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 967, Мерзляк, Полонский, Якир, Учебник
Номер 1004, Мерзляк, Полонский, Якир, Учебник
Номер 1083, Мерзляк, Полонский, Якир, Учебник
Номер 1090, Мерзляк, Полонский, Якир, Учебник
Номер 1091, Мерзляк, Полонский, Якир, Учебник
Номер 1101, Мерзляк, Полонский, Якир, Учебник
Номер 1115, Мерзляк, Полонский, Якир, Учебник
Номер 1118, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Упражнение 1050, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 347, Мерзляк, Полонский, Якир, Учебник
Номер 488, Мерзляк, Полонский, Якир, Учебник
Упражнение 192, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 708, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 713, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 724, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 833, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1276, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1315, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение стр. 171, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс