Линейное уравнение с двумя переменными и его график
Определение
Линейным уравнением с двумя переменными называют уравнение вида 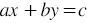 , где , где 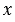 и и 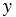 - переменные, - переменные, 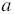 , , 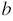 , , 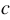 - некоторые числа. - некоторые числа. |
Случай 1:
Допустим нам задано линейное уравнение 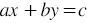 , в котором
, в котором 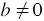 . Оставим в левой части уравнения слагаемые, которые содержат переменную
. Оставим в левой части уравнения слагаемые, которые содержат переменную 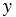 , остальные перенесем в правую часть, изменив их знак на противоположный, получим:
, остальные перенесем в правую часть, изменив их знак на противоположный, получим:
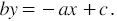
Так как по условию 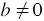 , то мы можем поделить обе части уравнения на
, то мы можем поделить обе части уравнения на 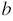 , то есть запишем:
, то есть запишем:
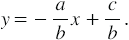
Обозначим коэффициенты следующим образом:
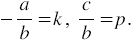
Тогда запишем
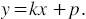
Но эта формула задает линейную функцию, графиком которой является невертикальная прямая, поэтому графиком уравнения 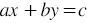 , где
, где 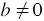 , является невертикальная прямая.
, является невертикальная прямая.
Пример 1. Построим график уравнения 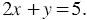
Решение: Данное уравнение является линейным уравнением с двумя переменными, у которого 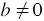 , значит, графиком данного уравнения является прямая, поэтому для построения графика достаточно определить координаты двух любых её точек. Если
, значит, графиком данного уравнения является прямая, поэтому для построения графика достаточно определить координаты двух любых её точек. Если 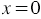 , то
, то  ; если
; если 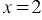 , то
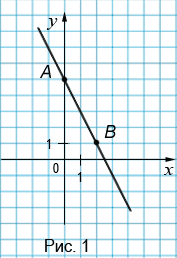
, то 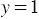 . Теперь через точки А(0; 5) и В(2; 1) проведем прямую (рис. 1). Полученная прямая будет являться искомым графиком.
. Теперь через точки А(0; 5) и В(2; 1) проведем прямую (рис. 1). Полученная прямая будет являться искомым графиком.
Случай 2:
Пусть задано линейное уравнение 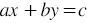 , в котором
, в котором 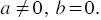 То есть мы получим уравнение вида
То есть мы получим уравнение вида 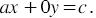
Пример 2. Построим график уравнения 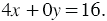
Решение: Найдем несколько решений данного уравнения:
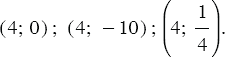
Очевидно, что любая пара чисел, которая имеет вид 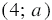 , и только она, где
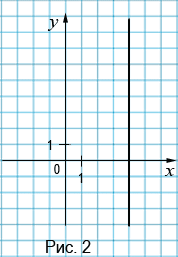
, и только она, где 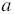 - произвольное число, является решением нашего уравнения. Откуда можно заключить, что искомый график содержит все точки, у которых абсцисса равна 4, а ордината - любое число, но все эти точки принадлежат прямой, которая перпендикулярна оси абсцисс и проходит через точку (4; 0) (рис. 2). Тогда решением данного уравнения будут пары чисел, которые являются координатами точек, принадлежащих полученной прямой.
- произвольное число, является решением нашего уравнения. Откуда можно заключить, что искомый график содержит все точки, у которых абсцисса равна 4, а ордината - любое число, но все эти точки принадлежат прямой, которая перпендикулярна оси абсцисс и проходит через точку (4; 0) (рис. 2). Тогда решением данного уравнения будут пары чисел, которые являются координатами точек, принадлежащих полученной прямой.
То есть графиком уравнения вида 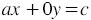 , где
, где 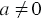 , является вертикальная прямая.
, является вертикальная прямая.
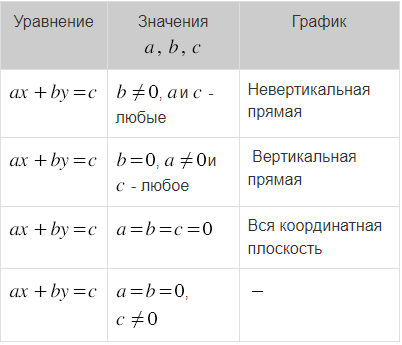
В каждом из двух случаев: 1) 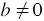 ; 2) ; 2) 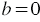 и и 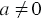 - графиком уравнения - графиком уравнения 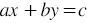 является прямая. является прямая. |
Случай 3:
Пусть задано линейное уравнение 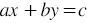 , в котором , то есть имеем Произведение любого числа на ноль равно нулю, а сумма двух выражений, равных нулю, равна нулю, значит, данное уравнение при не имеет решений, а значит, не существует точек, которые могли бы быть графиком данного уравнения.
, в котором , то есть имеем Произведение любого числа на ноль равно нулю, а сумма двух выражений, равных нулю, равна нулю, значит, данное уравнение при не имеет решений, а значит, не существует точек, которые могли бы быть графиком данного уравнения.
Если , то уравнение принимает вид:
В этом случае любая пара чисел будет являться решением данного уравнения, а значит, графиком уравнения будет являться вся координатная плоскость.
Советуем посмотреть:
Решение систем линейных уравнений методом подстановки
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Линейные неравенства с двумя переменными и их системы
Исследование системы двух линейных уравнений с двумя переменными
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 970, Мерзляк, Полонский, Якир, Учебник
Номер 973, Мерзляк, Полонский, Якир, Учебник
Номер 1024, Мерзляк, Полонский, Якир, Учебник
Номер 1035, Мерзляк, Полонский, Якир, Учебник
Номер 1053, Мерзляк, Полонский, Якир, Учебник
Номер 1062, Мерзляк, Полонский, Якир, Учебник
Номер 1070, Мерзляк, Полонский, Якир, Учебник
Номер 1092, Мерзляк, Полонский, Якир, Учебник
Номер 1111, Мерзляк, Полонский, Якир, Учебник
Упражнение 1165, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 91, Мерзляк, Полонский, Якир, Учебник
Номер 134, Мерзляк, Полонский, Якир, Учебник
Номер 173, Мерзляк, Полонский, Якир, Учебник
Номер 205, Мерзляк, Полонский, Якир, Учебник
Номер 302, Мерзляк, Полонский, Якир, Учебник
Номер 310, Мерзляк, Полонский, Якир, Учебник
Номер 371, Мерзляк, Полонский, Якир, Учебник
Упражнение 1314, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1315, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс