Решение систем линейных уравнений методом подстановки
Алгоритм решения системы линейных уравнений методом подстановки:
1) выразить из любого уравнения системы одну переменную через другую;
2) подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;
3) решить уравнение с одной переменной, полученное на втором шаге;
4) подставить найденное значение переменной в выражение, полученное на первом шаге;
5) вычислить значение другой переменной;
6) записать ответ.
Пример:
Решите систему уравнений методом подстановки
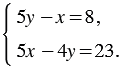
Решение:
Из первого уравнения системы, используя свойства уравнений, выразим переменную 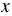 через переменную
через переменную 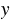 . Для этого перенесем в первом уравнении системы слагаемое 5
. Для этого перенесем в первом уравнении системы слагаемое 5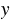 из левой части уравнения в правую, изменив при этом его знак:
из левой части уравнения в правую, изменив при этом его знак:
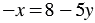 .
.
Теперь умножим обе части этого уравнения на 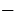 1, получим:
1, получим:
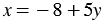 или
или 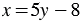 .
.
Подставим во второе уравнение системы вместо переменной 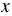 выражение
выражение 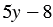 . Получим систему
. Получим систему
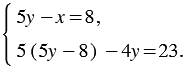
Эта и исходная система имеют одни те же решения.
Последнее уравнение полученной системы является уравнением с одной переменной. Решим его:
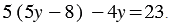
Используя распределительное свойство умножения, раскрываем скобки:
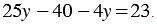
Перенесем слагаемое 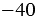 из левой части уравнения в правую, изменив при этом его знак:
из левой части уравнения в правую, изменив при этом его знак:
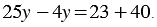
В левой части уравнения приводим подобные слагаемые:
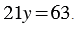
Мы получили линейное уравнение, которое имеет единственный корень: 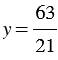 или, разделив числитель на знаменатель,
или, разделив числитель на знаменатель, 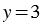 .
.
Подставим найденное значение переменной 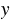 в уравнение
в уравнение 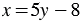 . Получим:
. Получим:
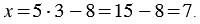
Пара чисел (7; 3) - искомое решение системы.
Обратите внимание, при записи решения системы в скобках на первом месте пишут значение 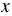 , на втором - значение
, на втором - значение 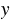 .
.
Советуем посмотреть:
Линейное уравнение с двумя переменными и его график
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Линейные неравенства с двумя переменными и их системы
Исследование системы двух линейных уравнений с двумя переменными
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 1037, Мерзляк, Полонский, Якир, Учебник
Номер 1054, Мерзляк, Полонский, Якир, Учебник
Номер 1059, Мерзляк, Полонский, Якир, Учебник
Номер 1060, Мерзляк, Полонский, Якир, Учебник
Номер 1067, Мерзляк, Полонский, Якир, Учебник
Номер 1234, Мерзляк, Полонский, Якир, Учебник
Упражнение 1088, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1094, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1189, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1237, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Упражнение 199, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 589, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 606, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 706, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 711, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 714, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 725, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 772, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 780, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1332, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс