Решение задач с помощью систем линейных уравнений

При решении некоторых задач системы двух линейных уравнений с двумя переменными используют как математические модели реальных ситуаций. В данной статье мы рассмотрим несколько примеров таких задач.

Пример 1. Мальвина продает розы и лилии, которые она выращивает в своем саду. Букет из 9 роз и 17 лилий стоит 52 сольдо. При этом 26 роз стоят дороже 17 лилий на 18 сольдо. Сколько стоит 1 роза и 1 лилия?

Решение. Пусть роза стоит 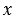сольдо, а лилия - 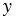сольдо. Тогда букет из из 9 роз и 17 лилий будет стоить  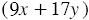сольдо, что по условию составляет 52 сольдо. Следовательно, 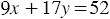. Также известно, что 26 роз стоят дороже 17 лилий на 18 сольдо. Тогда  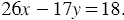Имеем систему уравнений:

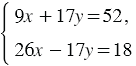
Решив эту систему, получаем, что 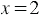, 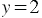. То есть мы получили, что и роза и лилия стоят 2 сольдо.

Пример 2. Найдите два числа, если их сумма равна 6, а их разность 8.

Решение. Пусть первое число равно 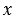, а другое - 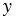. Тогда  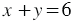 и . И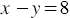меем систему уравнений:

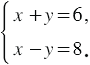
Решив эту систему, получаем, что 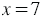,  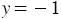. То есть сумма чисел 7 и -1 равна 6, а их разность 8.

Пример 3. Моторная лодка за 3 часа движения против течения реки и 2,5 часа по течению проходит 98 км. Найдите собственную скорость лодки и скорость течения, если за 5 часов движения по течению она проходит на 36 км больше, чем за 4 часа против течения реки.

Решение. Пусть собственная скорость лодки равна 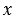км/ч, а скорость течения равна 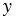км/ч. Тогда скорость лодки по течению равна 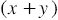км/ч, а скорость лодки против течения 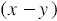км/ч. Тогда за три часа движения против течения реки лодка пройдет 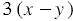км, а за 2,5 часа по течению 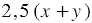км. Сумма этих расстояний по условию равна 98 км, поэтому 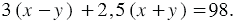За 5 часов движения по течению лодка проходит 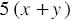км, а за 4 часа против течения - 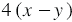км. Так как за 5 часов движения по течению она проходит на 36 км больше, чем за 4 часа против течения реки, то 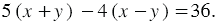Имеем систему уравнений:

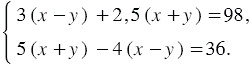
Решив эту систему, получаем, что 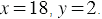То есть мы получили, что собственная скорость лодки равна 18 км/ч, а скорость течения реки равна 2 км/ч.