Упражнение 332 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 106

а) \(x^2 = \dfrac{7x - 4}{4x - 7}\)   \(/\times 4x - 7\)

ОДЗ: \(4x - 7 \ne 0\)

          \(4x \ne 7\)

          \(x \ne \dfrac{7}{4}\)

          \(x \ne 1,75.\)

\[ x^2(4x - 7) = 7x - 4 \]

\( 4x^3 - 7x^2 - 7x + 4 = 0 \)

\(\pm1; \pm2; \pm4\) - делители числа 4.

Если \(x = -1\), то

\(4\cdot(-1)^3 - 7\cdot(-1)^2 - 7\cdot(-1) + 4 = 0\)

\(-4 - 7 + 7 + 4 = 0\)

\(0 = 0\) - верно.

\(x = -1\) - корень уравнения.

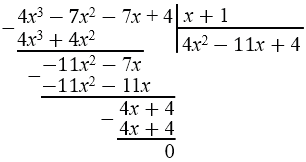
\( 4x^3 - 7x^2 - 7x + 4 = (x+1)(4x^2 - 11x + 4)\)

\(4x^2 - 11x + 4 = 0\)

\(D = (-11)^2 - 4\cdot4\cdot4 = \)

\( = 121 - 64 = 57 > 0\) - 2 корня.

\(x_{1,2} = \frac{11 \pm \sqrt{57}}{2\cdot4} =\frac{11 \pm \sqrt{57}}{8} \)

Ответ: \(-1,\; \frac{11 + \sqrt{57}}{8};\, \frac{11 - \sqrt{57}}{8}.\)

б) \(x^2 = \dfrac{5x - 3}{3x - 5}\)   \(/\times3x-5\)

ОДЗ: \(3x - 5 \ne 0 \)

          \(3x \ne5\)

          \(x \ne \dfrac{5}{3}\)

          \(x \ne 1\dfrac{2}{3}\)

\( x^2(3x - 5) = 5x - 3 \)

\( 3x^3 - 5x^2 - 5x + 3 = 0 \)

\(\pm1; \pm3\) - делители числа 3.

Если \(x = -1\), то

\(3\cdot(-1)^3 - 5\cdot(-1)^2 - 5\cdot(-1) + 3 = 0\)

\(-3 - 5 + 5 + 3 = 0\)

\(0 = 0\) - верно.

\(x = -1\) - корень уравнения.

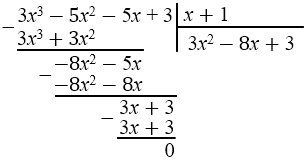
\( 3x^3 - 5x^2 - 5x + 3 = (x+1)(3x^2-8x+3) \)

\((x+1)(3x^2-8x+3) =0\)

\(3x^2-8x+3 =0\)

\(D=(-8)^2 -4\cdot3\cdot3 =\)

\(=64 - 36 = 28>0\) - 2 корня.

\(\sqrt{28} = \sqrt{4\cdot7} = 2\sqrt7\).

\(x_{1,2}=\frac{8\pm2\sqrt7}{2\cdot3} = \frac{8\pm2\sqrt7}{6} =\)

\(=\frac{\cancel2(4\pm\sqrt7)}{\cancel6_ {\color{blue}{3}} } =\frac{4\pm\sqrt7}{3} .\)

Ответ: \(-1,\; \frac{4-\sqrt7}{3};\, \frac{4+\sqrt7}{3}.\)

Пояснения:

Алгоритм решения уравнений:

1)  найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

В каждом случае получили кубическое уравнение.

Если многочлен имеет целый корень, то он является делителем свободного члена (последнего числового коэффициента). Поэтому для уравнений с целыми коэффициентами удобно проверять несколько простых значений \(x\) (например, \(\pm1, \pm2, \pm3,\dots\)). Найденное значение, при котором многочлен обращается в ноль, даёт линейный множитель

\((x - x_0)\).

После нахождения корня \(x_0\) мы делим многочлен на \((x - x_0)\) (столбиком) и получаем многочлен меньшей степени. Процесс можно повторять, пока степень не станет 2, а затем решить квадратное уравнение.

Квадратное уравнение

\(ax^{2} + bx + c = 0\)

решается через дискриминант

\(D = b^2 - 4ac\).

Если \(D > 0\), то уравнение имеет 2 корня:

\[ x_{1,2} = \dfrac{-b \pm \sqrt{D}}{2a}. \]