Упражнение 1135 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1135 учебника 2023-2025 (стр. 224):
Имеется молоко 5%-й жирности и 1%-й жирности. Сколько молока каждого вида надо взять, чтобы получить 3 л молока, жирность которого составляет 3,2%?
№1135 учебника 2013-2022 (стр. 226):
Изобразите на координатной плоскости фигуру, которую задаёт система неравенств
\( \begin{cases} y \le -0,5x + 2,\\ x \ge 0,\\ y \ge 0, \end{cases} \)
и найдите её площадь.
Подсказка
№1135 учебника 2023-2025 (стр. 224):
Вспомните:
- Решение задач с помощью системы уравнений.
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Проценты.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Вычитание десятичных дробей.
- Подобные слагаемые.
№1135 учебника 2013-2022 (стр. 226):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
- Умножение рациональных чисел.
- Прямоугольный треугольник.
- Как найти площадь прямоугольника.
- Умножение обыкновенных дробей.
Ответ
№1135 учебника 2023-2025 (стр. 224):
Пусть \(x\) (л) — объём молока 5%-й жирности, а \(y\) (л)— объём молока 1%-й жирности.
Составим систему уравнений:
\( \begin{cases} x + y = 3,\\ 0{,}05x + 0{,}01y = 0{,}032 \cdot 3. \end{cases} \)
\( \begin{cases} x + y = 3,\\ 0{,}05x + 0{,}01y = 0{,}096 /\times(-100) \end{cases} \)
\( \begin{cases} x + y = 3,\\ -5x - y = -9,6 \end{cases} \)
\( \begin{cases} -4x= -6,6 \\ x + y = 3 \end{cases} \)
\( \begin{cases} x= \frac{6,6}{4} \\ y = 3 - x \end{cases} \)
\( \begin{cases} x=1,65 \\ y = 3 - 1,65 \end{cases} \)
\( \begin{cases} x=1,65 \\ y = 1,35 \end{cases} \)
| - | 6 | 6 | 4 | ||||||||||||
| 4 | 1 | 6 | 5 | ||||||||||||
| - | 2 | 6 | |||||||||||||
| 2 | 4 | ||||||||||||||
| - | 2 | 0 | |||||||||||||
| 2 | 0 | ||||||||||||||
| 0 |
Ответ: нужно взять 1,65 л молока 5%-й жирности и 1,35 л молока 1%-й жирности.
Пояснения:
Использованные приёмы:
1) Введение переменных \(x\) и \(y\) для объёмов молока двух жирностей.
2) Составление системы по сумме объёмов и по суммарному содержанию жира.
3) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
4) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
5) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
6) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
№1135 учебника 2013-2022 (стр. 226):
\( \begin{cases} y \le -0,5x + 2,\\ x \ge 0,\\ y \ge 0 \end{cases} \)
\(y = -0,5x + 2\)
| \(x\) | 0 | 4 |
| \(y\) | 2 | 0 |
\( \begin{cases} x \ge 0,\\ y \ge 0 \end{cases} \) - I координатная четверть.
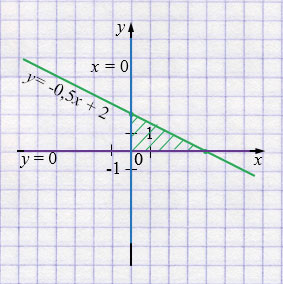
Область пересечения - прямоугольный треугольник.
\(S = \frac{1}{2}\cdot2 \cdot 4 = 4.\)
Ответ: площадь равна 4.
Пояснения:
Использованные правила и формулы:
– Пересечение полуплоскостей даёт геометрическую фигуру - прямоугольный треугольник.
– Площадь прямоугольника равна произведению его длины и ширины. Площадь прямоугольного треугольника равна половине площади прямоугольника, для которого катеты прямоугольного треугольника являются длиной и шириной. Значит, площадь прямоугольного треугольника равна половине произведения его катетов.
Подробности шагов:
Сначала выделили границы \(x\ge0\) и \(y\ge0\) — первая четверть координатной плоскости.
Затем прямая \(y=-0,5x+2\) ограничивает область сверху.
Решение системы неравенств - область пересечения - прямоугольный треугольник.
Катеты этого треугольника лежат вдоль осей \(Ox\) и \(Oy\) с длинами 4 и 2 соответственно.
Поэтому площадь равна половине произведения этих катетов.
Вернуться к содержанию учебника