Деление десятичных дробей
Пусть хотя бы одно из чисел 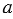 ,
, 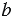 ,
, 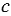 является десятичной дробью, тогда разделить число
является десятичной дробью, тогда разделить число 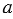 на число
на число 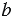 - значит найти такое число
- значит найти такое число 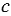 , которое при умножении на
, которое при умножении на 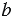 даёт число
даёт число 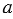 .
.
Рассмотрим деление десятичной дроби на натуральное число:
Пример 1: Найдём частное 143,64 : 4.
Выполним данный пример, используя деление уголком, не обращая внимания на запятую:
| - | 1 | 4 | 3 | 6 | 4 | 4 | |||||
| 1 | 2 | 3 | 5 | 9 | 1 | ||||||
| - | 2 | 3 | |||||||||
| 2 | 0 | ||||||||||
| - | 3 | 6 | |||||||||
| 3 | 6 | ||||||||||
| - | 4 | ||||||||||
| 4 | |||||||||||
| 0 |
Рассмотрим подробно: целая часть делимого равна 143. Разделим 143 на 4. 1 меньше 4, то есть первое неполное делимое - это 14. Ближайшее число, меньшее 14, которое делится на 4, - это 12, значит, в частное записываем 3, а из 14 вычитаем 12, в остатке получаем 2.
Сносим 3, второе неполное делимое - 23. Ближайшее число, меньшее 23, которое делится на 4, - это 20, значит, в частное записываем 5, из 23 вычитаем 20, в остатке получаем 3. В целой части знаки закончились, далее переходим к делению дробной части, но перед этим в частном ставим запятую.
Сносим 6, третье неполное делимое - 36. 36 делится на 4 нацело: 36 : 4 = 9. В частное после запятой записываем 9. Из 36 вычитаем 36, так как в делителе не закончились цифры, то ноль не пишем, а сносим 4 - четвертое неполное делимое. 4 : 4 = 1, в частное записываем 1, в остаток 0. Когда в остатке остается 0 и цифр в делимом не останется, деление заканчивается. Итак, мы получили, что 143,64 : 4 = 35,91.
|
Чтобы разделить десятичную дробь на натуральное число, нужно: 1) разделить дробь на это число, не обращая внимания на запятую; 2) поставить в частном запятую, когда кончится деление целой части. |
Мы рассмотрели пример, когда целая часть делимого больше делителя, если целая часть делимого меньше делителя, то целая часть частного будет равна нулю.
Пример 2: Найдём частное 5,418 : 14.
| - | 5 | 4 | 1 | 8 | 1 | 4 | ||||
| 4 | 2 | 0 | 3 | 8 | 7 | |||||
| - | 1 | 2 | 1 | |||||||
| 1 | 1 | 2 | ||||||||
| - | 9 | 8 | ||||||||
| 9 | 8 | |||||||||
| 0 |
Пример 3: Найдём частное 0,4488 : 12.
| - | 0 | 4 | 4 | 8 | 8 | 1 | 2 | |||||
| 3 | 6 | 0 | 0 | 3 | 7 | 4 | ||||||
| - | 8 | 8 | ||||||||||
| 8 | 4 | |||||||||||
| - | 4 | 8 | ||||||||||
| 4 | 8 | |||||||||||
| 0 |
Пример 4: Найдём частное 32,86 : 5.
| - | 3 | 2 | 8 | 6 | 5 | |||||
| 3 | 0 | 6 | 5 | 7 | ||||||
| - | 2 | 8 | ||||||||
| 2 | 5 | |||||||||
| - | 3 | 6 | ||||||||
| 3 | 5 | |||||||||
| 1 |
Мы видим, что цифры в делимом закончились, но при этом остаток не равен 0. То есть деление не окончено. В таких случаях пользуемся тем, что, если приписать справа от десятичной дроби сколько угодно нулей, дробь не изменится, а, значит, числа делителя не могут закончиться. Тогда получаем:
| - | 3 | 2 | 8 | 6 | 5 | |||||
| 3 | 0 | 6 | 5 | 7 | 2 | |||||
| - | 2 | 8 | ||||||||
| 2 | 5 | |||||||||
| - | 3 | 6 | ||||||||
| 3 | 5 | |||||||||
| - | 1 | 0 | ||||||||
| 1 | 0 | |||||||||
| 0 |
Мы знаем, что одно натуральное число не всегда делится на другое нацело. Рассмотрим такой пример.
Пример 5: Найдем частное 37 : 2.
| - | 3 | 7 | 2 | |||
| 2 | 1 | 8 | ||||
| - | 1 | 7 | ||||
| 1 | 6 | |||||
| 1 |
Мы видим, что цифры в делимом закончились, но при этом остаток не равен 0. То есть деление не окончено. Но нам известно, что любое натуральное число можно записать в виде десятичной дроби, поставив запятую после данного числа и после нее подписав необходимое количество нулей, тогда имеем:
| - | 3 | 7 | 0 | 2 | ||||
| 2 | 1 | 8 | 5 | |||||
| - | 1 | 7 | ||||||
| 1 | 6 | |||||||
| - | 1 | 0 | ||||||
| 1 | 0 | |||||||
| 0 |
Пример 6: Найдём частное 1 : 160.
| - | 1 | 1 | 6 | 0 | |||
| 0 |
Делитель больше делимого, значит, в частное записываем 0, затем ставим запятую. Нам известно, что любое натуральное число можно записать в виде десятичной дроби, поставив запятую после данного числа и после нее подписав необходимое количество нулей, записываем в делимом 0, получаем:
| - | 1 | 0 | 1 | 6 | 0 | ||
| 0 | 0 |
10 меньше 160, значит, в частное записываем 0 и дописываем 0 в делителе, получаем:
| - | 1 | 0 | 0 | 1 | 6 | 0 | |||
| 0 | 0 | 0 |
100 меньше 160, значит, в частное записываем 0 и дописываем 0 в делителе, получаем:
| - | 1 | 0 | 0 | 0 | 1 | 6 | 0 | |||
| 9 | 6 | 0 | 0 | 0 | 0 | 6 | ||||
| 4 | 0 |
1000 больше 160, значит, ищем наибольшее число, меньшее 1000, которое делится на 160 - это число 960, 960 : 160 = 6. Записываем неполное делимое, а в частное 6, получаем в остатке 40, дописываем 0, продолжаем деление и получаем:
| - | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 6 | 0 | |||||
| 9 | 6 | 0 | 0 | 0 | 0 | 6 | 2 | 5 | ||||||
| - | 4 | 0 | 0 | |||||||||||
| 3 | 2 | 0 | ||||||||||||
| - | 8 | 0 | 0 | |||||||||||
| 8 | 0 | 0 | ||||||||||||
| 0 |
Правило деления десятичных дробей на на 0,1; 0,01; 0,001 и т.д.:
| Чтобы разделить десятичную дробь на 0,1, 0,01, 0,001 и т. д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т. д. цифры. |
Правило деления десятичных дробей на на 10; 100; 1 000 и т.д.:
| Чтобы разделить десятичную дробь на 10, 100, 1 000 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры. |
Зная это правило, можно следующий следующий вывод:
Если делимое и делитель увеличить одновременно в 10, 100, 1 000 и т. д. раз, то частное не изменится.
Пример 7: Найдем частное 14,364 : 0,4.
Увеличим делимое и делитель одновременно в 10 раз. Тогда получим: 14,364 : 0,4 = 143,64 : 4.
Деление десятичной дроби 143,64 на 4 у нас выполнено выше, значит, мы можем записать, что 14,364 : 0,4 = 143,64 : 4 = 35,91.
Правило деления десятичной дроби на десятичную дробь:
|
Чтобы разделить десятичную дробь на десятичную, нужно: 1) перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; 2) выполнить деление на натуральное число. |
Советуем посмотреть:
Десятичная запись дробных чисел
Сложение и вычитание десятичных дробей
Приближенные значения чисел. Округление чисел
Правило встречается в следующих упражнениях:
5 класс
Задание 1647, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1689, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.297, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.428, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.28, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 1107, Мерзляк, Полонский, Якир, Учебник
Номер 1205, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 131, Мерзляк, Полонский, Якир, Учебник
Номер 502, Мерзляк, Полонский, Якир, Учебник
Номер 568, Мерзляк, Полонский, Якир, Учебник
Номер 702, Мерзляк, Полонский, Якир, Учебник
Номер 1157, Мерзляк, Полонский, Якир, Учебник
Задание 656, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.560, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.1, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.160, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.9, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 40, Мерзляк, Полонский, Якир, Учебник
Номер 107, Мерзляк, Полонский, Якир, Учебник
Номер 347, Мерзляк, Полонский, Якир, Учебник
Номер 946, Мерзляк, Полонский, Якир, Учебник
Номер 1052, Мерзляк, Полонский, Якир, Учебник
Упражнение 14, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 312, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 480, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 762, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 183, Макарычев, Миндюк, Учебник
8 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 521, Мерзляк, Полонский, Якир, Учебник
Упражнение 74, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 188, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 498, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 595, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 717, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 989, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 990, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1169, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс