Умножение обыкновенных дробей
| Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. |
Примеры:
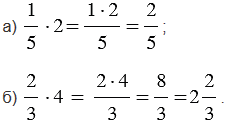
Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.
Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Пример:
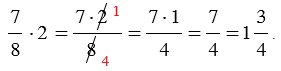
| Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей. |
Пример:
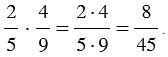
Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Примеры:
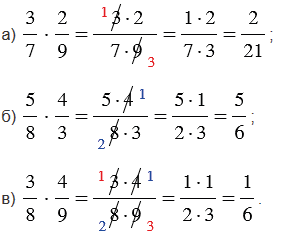
Умножение смешанных чисел
| Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. |
Примеры:

Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.
Примеры:
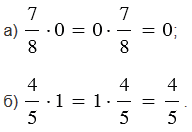
| Чтобы умножить смешанное число на натуральное число, можно представить смешанное число в виде неправильной дроби, а затем воспользоваться правилом умножения дроби на натуральное число или можно умножить целую часть на натуральное число, далее умножить дробную часть на натуральное число и полученные произведения сложить. |
Пример:
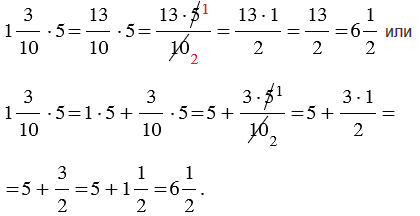
Нахождение дроби от числа
| Чтобы найти дробь от числа, нужно умножить число на эту дробь. |
Примеры:
а) Найти 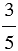 от числа 20.
от числа 20.
Решение:
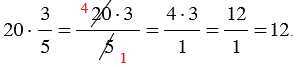
б) Найти 0,6 от числа 9.
Решение:
90,6 = 5,4.
в) Найти 30 % от числа 500.
Решение:
1) 30% = 30 : 100 = 0,30 = 0,3
2) 5000,3 = 150.
Взаимно обратные числа
| Два числа, произведение которых равно 1, называют взаимно обратными. |
Примеры:
1) 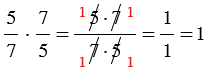 , значит, числа
, значит, числа 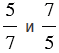 - взаимно обратные;
- взаимно обратные;
2) 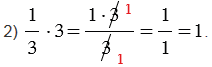
Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.
Пример:
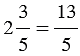 , значит, числу
, значит, числу 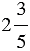 обратно число
обратно число 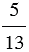 .
.
Запомните:
- Числом, обратным 1, является само число 1.
- Для числа 0 обратного числа не существует.
- Обратным числу
 является число
является число 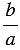 .
. - Если
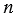 - натуральное число, то обратным ему является число
- натуральное число, то обратным ему является число 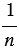 .
.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 567, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5.486, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.512, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.521, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.524, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.525, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.526, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.547, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.550, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.562, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 429, Мерзляк, Полонский, Якир, Учебник
Номер 1028, Мерзляк, Полонский, Якир, Учебник
Задание 569, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 596, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1317, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1431, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1493, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 13, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 5.63, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 386, Мерзляк, Полонский, Якир, Учебник
Номер 495, Мерзляк, Полонский, Якир, Учебник
Номер 646, Мерзляк, Полонский, Якир, Учебник
Номер 1036, Мерзляк, Полонский, Якир, Учебник
Упражнение 148, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 570, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 664, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 770, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1091, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1123, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 135, Мерзляк, Полонский, Якир, Учебник
Номер 171, Мерзляк, Полонский, Якир, Учебник
Номер 226, Мерзляк, Полонский, Якир, Учебник
Номер 280, Мерзляк, Полонский, Якир, Учебник
Упражнение 373, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 692, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 878, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 879, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1031, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1054, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс