Упражнение 1133 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1133 учебника 2023-2025 (стр. 224):
Под озимыми культурами было занято на 480 га больше, чем под яровыми. После того как убрали 80 % озимых и 25 % яровых культур, площадь, оставшаяся под озимыми, оказалась на 300 га меньше, чем площадь под яровыми. Какая площадь была отведена под яровые и какая под озимые культуры?
№1133 учебника 2013-2022 (стр. 226):
Изобразите на координатной плоскости множество точек, которое задаёт система неравенств:
а) \(\displaystyle \begin{cases}y \le -x,\\y \ge -5;\end{cases}\)
б) \(\displaystyle \begin{cases}y \ge x - 2,\\y \le x + 3;\end{cases}\)
в) \(\displaystyle \begin{cases}y \ge -2x + 4,\\y \le x + 1.\end{cases}\)
Подсказка
№1133 учебника 2023-2025 (стр. 224):
Вспомните:
- Решение задач с помощью системы уравнений.
- Что называют решением системы уравнений.
- Способ сложения при решении систем уравнений.
- Проценты.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Умножение десятичных дробей.
- Деление десятичных дробей.
- Подобные слагаемые.
№1133 учебника 2013-2022 (стр. 226):
Вспомните:
- Что называют решением системы неравенств с двумя переменными.
- График линейной функции.
- Координаты точки.
- Сложение рациональных чисел.
Ответ
№1133 учебника 2023-2025 (стр. 224):
100% - 80% = 20% = 0,2 - площади осталось убрать под озимыми культурами.
100% - 25% = 75% = 0,75 - площади осталось убрать под яровыми культурами.
Пусть \(x\) (га) — площадь под озимыми, а \(y\) (га) — площадь под яровыми, тогда \(0,3x\) (га) — осталось убрать под озимыми, а \(0,75y\) (га) — осталось убрать под яровыми.
Составим систему уравнений:
\( \begin{cases} x - y = 480,\\ 0{,}75y - 0{,}2x = 300 /\times5 \end{cases} \)
\( \begin{cases} x - y = 480,\\ -x + 3,75y = 1500 \end{cases} \)
\( \begin{cases} 2,75y =1980,\\ -x + 3,75y = 1500 \end{cases} \)
\( \begin{cases} y =\frac{980}{2,75},\\ -x + 3,75y = 1500 \end{cases} \)
\( \begin{cases} y =\frac{98000}{275},\\ x = 3,75y - 1500 \end{cases} \)
\( \begin{cases} y =720,\\ x = 3,75\cdot720 - 1500 \end{cases} \)
\( \begin{cases} y =720,\\ x = 2700 - 1500 \end{cases} \)
\( \begin{cases} y =720,\\ x = 1200 \end{cases} \)
|
|
Ответ: под яровые культуры отведено 720 га, под озимые - 1200 га.
Пояснения:
Использованные приёмы:
1) Введение переменных \(x\) и \(y\) для исходных площадей.
2) Перевод условий задачи в систему уравнений:
– разность площадей:
\(x - y = 480\);
– после уборки: 20 % от \(x\) стало на 300 га меньше, чем 75 % от \(y\):
\(0{,}75y - 0{,}2x = 300\).
3) Решение системы методом сложения: складываем почленно уравнения системы так, чтобы в новом уравнении исчезла одна из переменных. Там, где необходимо, одно из уравнений или оба уравнения делим или умножаем на числа так, чтобы перед одной из переменных получить противоположные коэффициенты, которые при сложении приведут к сокращению выражений с этой переменной.
4) После сложения уравнений системы получается линейное уравнение с одной переменной, решение которого дает значение этой переменной.
5) Уравнение вида \(ax = b\) называется линейным и при \(a \neq 0\) имеет единственный корень \(x=\frac{b}{a}\).
6) Подстановка: после нахождения одной переменной подставляем её значение в одно из исходных уравнений для вычисления значения второй переменной.
№1133 учебника 2013-2022 (стр. 226):
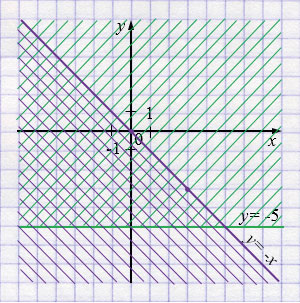
а) \(\displaystyle \begin{cases}y \le -x,\\y \ge -5\end{cases}\)
\(y = -x\)
| \(x\) | 0 | 3 |
| \(y\) | 0 | -3 |
б) \(\displaystyle \begin{cases}y \ge x - 2,\\y \le x + 3\end{cases}\)
\(y = x - 2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | 0 |
\(y = x + 3\)
| \(x\) | 0 | -3 |
| \(y\) | 3 | 0 |

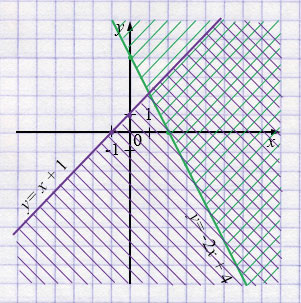
в) \(\displaystyle \begin{cases}y \ge -2x + 4,\\y \le x + 1\end{cases}\)
\(y = -2x + 4\)
| \(x\) | 0 | 2 |
| \(y\) | 4 | 0 |
\(y = x + 1\)
| \(x\) | 0 | -1 |
| \(y\) | 1 | 0 |
Пояснения:
1) Для каждого неравенства проводим соответствующую прямую по двум точкам и определяем, какую сторону штриховать, проверяя точку (например, \((0,0)\)).
2) При знаках «\(\ge\)» и «\(\le\)» граница включается (сплошная линия).
3) Решение системы - пересечение штрихованных областей.
а) Границы: прямая \(y=-x\) и горизонтальная прямая \(y=-5\). Поскольку знак «\(\le\)» у первой, штрихуем область ниже или на линии \(y=-x\). Поскольку знак «\(\ge\)» у второй, штрихуем область выше или на линии \(y=-5\). Итоговая область — полоса между этими прямыми, включая границы.
б) Границы: прямая \(y=x-2\) и прямая \(y=x+3\). Для «\(\ge\)» у первой — штриховка над или на \(y=x-2\). Для «\(\le\)» у второй — штриховка под или на \(y=x+3\). Итоговая область — полоса между этими параллельными прямыми, включая их.
в) Границы: прямая \(y=-2x+4\) и прямая \(y=x+1\). Для «\(\ge\)» у первой — штриховка над или на \(y=-2x+4\). Для «\(\le\)» у второй — штриховка под или на \(y=x+1\). Область — перекрытие двух полуплоскостей, включая границы.
Вернуться к содержанию учебника