Решение уравнений / Рациональные числа / Справочник по математике 5-9 класс

Нам известно, что решить уравнение - значит найти все его корни или показать, что их нет вообще. Для нахождения корней уравнения мы используем правила нахождения неизвестного слагаемого, вычитаемого, множителя и т.д.. Но часто мы не можем решить уравнение, используя данные правила, например, как найти корни уравнения 4 + 2 = 7?

Нам известно, что если к равным числам прибавить одно и то же число, то получатся равные числа, в буквенном виде мы это можем записать так:

если 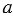= 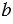, то 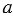+ 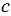= 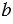+ 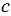. Данное утверждение называют свойством равенства. Для уравнения также будет справедливо то, что:

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получится уравнение, имеющее те же корни, что и данное.

Используя это утверждение, решим наше уравнение, вычтем из левой и правой частей данного уравнения число и 2, получим 4 + 22 = 72 или 3= 9. Теперь мы можем решить данное уравнение, используя правило нахождения неизвестного множителя получим: = 3.

Рассмотрим уравнение 4= 9, применим наше утверждение к этому уравнению. Прибавим к обеим частям уравнения число (). Получим:

4+ () = 9 + () или 4 = 9. Такое же уравнение мы получим из уравнения 4= 9, перенеся из правой части уравнения в левую слагаемое , изменив его знак на противоположный. Решив уравнение 4 = 9, получим, что = 3.

Подставим данный корень в уравнение 4= 9, получим 4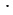(3) = (3)9 или 12 = 12, так как мы получили верное равенство, то число (3) является и корнем уравнения 4= 9. Из этого мы делаем вывод:

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

Решим уравнение:

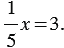
Найдем неизвестный множитель:

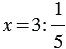или ,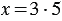

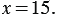
Данный результат мы можем получить, умножив обе части данного уравнения на 5, то есть:

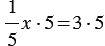или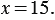

Из этого мы можем сделать вывод, что:

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

Советуем посмотреть:

Положительные и отрицательные числа. Координаты на прямой

Модуль числа

Рациональные числа

Сравнение рациональных чисел

Сложение рациональных чисел

Вычитание рациональных чисел

Умножение рациональных чисел

Деление рациональных чисел

Свойства действий с рациональными числами

Раскрытие скобок

Рациональные числа

Правило встречается в следующих упражнениях:

6 класс

Номер 1154, Мерзляк, Полонский, Якир, Учебник

Номер 1155, Мерзляк, Полонский, Якир, Учебник

Номер 1195, Мерзляк, Полонский, Якир, Учебник

Номер 1200, Мерзляк, Полонский, Якир, Учебник

Номер 1201, Мерзляк, Полонский, Якир, Учебник

Номер 1241, Мерзляк, Полонский, Якир, Учебник

Задание 1344, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1380, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1458, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1513, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 105, Мерзляк, Полонский, Якир, Учебник

Номер 532, Мерзляк, Полонский, Якир, Учебник

Номер 538, Мерзляк, Полонский, Якир, Учебник

Номер 591, Мерзляк, Полонский, Якир, Учебник

Номер 852, Мерзляк, Полонский, Якир, Учебник

Номер 1060, Мерзляк, Полонский, Якир, Учебник

Номер 1091, Мерзляк, Полонский, Якир, Учебник

Номер 1098, Мерзляк, Полонский, Якир, Учебник

Номер 1099, Мерзляк, Полонский, Якир, Учебник

Номер 1108, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 65, Мерзляк, Полонский, Якир, Учебник

Номер 170, Мерзляк, Полонский, Якир, Учебник

Номер 215, Мерзляк, Полонский, Якир, Учебник

Номер 412, Мерзляк, Полонский, Якир, Учебник

Номер 467, Мерзляк, Полонский, Якир, Учебник

Номер 629, Мерзляк, Полонский, Якир, Учебник

Номер 661, Мерзляк, Полонский, Якир, Учебник

Номер 686, Мерзляк, Полонский, Якир, Учебник

Номер 865, Мерзляк, Полонский, Якир, Учебник

Номер 890, Мерзляк, Полонский, Якир, Учебник