Упражнение 154 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник

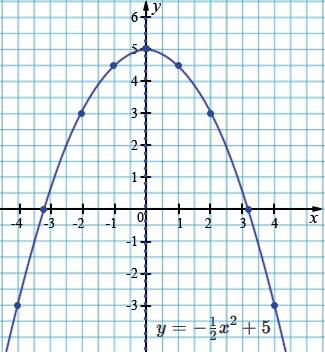
а) \( y=-\tfrac12 x^2 + 5\)

1. Графиком данной функции является парабола, ветви которой направлены вниз  \((a=-\tfrac12<0).\)

2. \( m=-\frac{b}{2a}=-\frac{0}{2\cdot\left(-\frac12\right)}=0. \)

\(n=-\tfrac12\cdot 0^2 + 5=5.\)

Вершина параболы: \((0; 5)\). Прямая \(x=0\) - ось симметрии параболы.

3. Нули функции:

\(-\tfrac12 x^2 + 5=0\)    \(|\times(-2)\)

\(x^2 -10=0\)

\((x- \sqrt {10})(x+\sqrt {10})=0\)

\(x- \sqrt {10}=0\) или \(x+\sqrt {10}=0\)

\(x=\sqrt {10}\)               \(x=-\sqrt {10}\)

\(x=3,2\)                 \(x=-3,2\)

\((-3,2; 0)\) и \((3,2; 0)\) - точки пересечения с осью \(x\).

4. Точка пересечения с осью \(y\): \((0; 5)\)

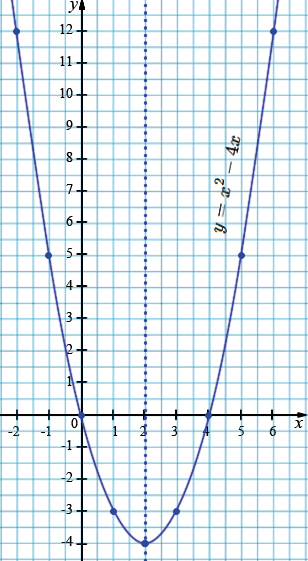
б) \( y=x^2 - 4x\)

1. Графиком данной функции является парабола, ветви которой направлены вверх \((a=1>0).\)    

2. \(m = -\frac{b}{2a} = \frac{4}{2} = 2 \)

\(n = 2^2 - 4\cdot 2 = 4 - 8 = -4. \)

Вершина параболы: \((2; -4)\). Прямая \(x=2\) - ось симметрии параболы.

3. Нули функция:

\(x^2 - 4x=0\)

\(x(x-4)=0\)

\(x=0\)   или   \(x-4=0\)

                       \(x=4\)

\((0; 0)\) и \((4; 0)\) - точки пересечения с осью \(x\).

4. Точка пересечения с осью \(y\): \((0; 0).\)

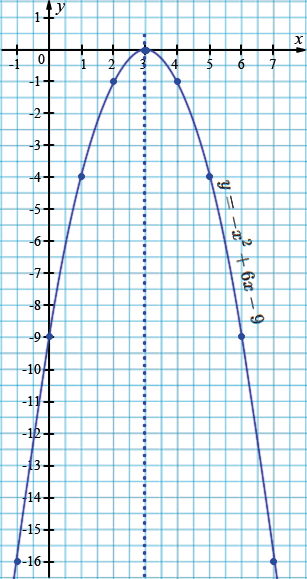
в) \( y = -x^2 + 6x - 9 \)

1. Графиком данной функции является парабола, ветви которой направлены вниз \((a=-1<0)\).

2. \(m = -\frac{6}{2\cdot(-1)} = 3\)

\(n = -(3^2) + 6\cdot 3 - 9 =\)

\(=-9 + 18 - 9 = 0. \)

Вершина параболы: \((3; 0)\). Прямая \(x=3\) - ось симметрии параболы.

3. Нули функции:

\(-x^2 + 6x - 9 = 0\)

\(x^2 - 6x + 9 = 0\)

\((x-3)^2= 0\)

\(x-3= 0\)

\(x=3\).

\((3; 0)\) - точка пересечения с осью \(x\).

4. Точка пересечения с осью \(y\):

\(x=0\): \( y = -0^2 + 6\cdot0 - 9=-9 \)

\((0; -9)\).

Пояснения:

1. Формула вершины параболы \((m; n)\):

\[ m = -\frac{b}{2a},\qquad n = f(m). \]

Это справедливо для любой функции вида \[ y = ax^2 + bx + c. \]

2. Ось симметрии

Ось симметрии — вертикальная прямая: \( x = m\).

3. Направление ветвей

• если \(a > 0\) — ветви вверх;

• если \(a < 0\) — ветви вниз.

\(m = 700\) г,  \(x = 10\) см

\( m = \rho V = \rho x^3 \)

\( 700 = \rho \cdot 10^3 \)

\( 700 = 1000\rho \)

\(\rho = \frac{700}{1000}\)

\(\rho = 0{,}7 \)

\( m = 0{,}7 x^3 \)

а) Если \( x= 2 \) см, то \( m =  5{,}6 \) г.

Если \( x = 5 \) см, то \( m =  87{,}5 \) г.

б) Если \( m = 30 \) г, то \( x \approx 3{,}5 \) см.

Если \( m = 100 \) г, то \( x \approx 5{,}2 \) см.

Пояснения:

Формула массы куба:

Масса пропорциональна объёму, а именно масса тела \(m\) равна произведению его плотности \(\rho\) и объема \(V\):

\( m = \rho V \).

Учитывая то, что объем куба равен кубу его ребра, масса куба:

\(m =\rho x^3 \),

где \(x\) - ребро куба.

Нахождение плотности:

Подставляем известные значения:

\( 700 = \rho \cdot 10^3 \), откуда \(\rho = 0{,}7 \).

Получаем зависимость:

\[ m = 0{,}7 x^3. \]

Чтобы построить график полученной зависимости, составляем таблицу, отмечаем точки на координатной плоскости и соединяем плавной линией (учитываем то, что \(x \ge 0\)).

Затем по графику находим значения \(m\) для известных \(x\) и наоборот.