Упражнение 1146 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник. Страница 257
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1146 учебника 2023-2025 (стр. 257):
В равнобедренном треугольнике \(ABC\) основание \(AC\) равно \( 6\) см, а боковая сторона — \(5\) см. Концы подвижного отрезка, параллельного основанию, лежат на боковых сторонах. Его длина равна \(y\) (см), а расстояние от вершины — \(x\) (см). Задайте формулой \(y\) как функцию от \(x\). Найдите множество значений этой функции.
№1146 учебника 2013-2022 (стр. 257):
Пересекает ли график функции \(y = \dfrac{3x + 1}{x}\) прямую:
а) \(x = 0\);
б) \(y = 0\);
в) \(x = 3\);
г) \(y = 3\)?
Подсказка
№1146 учебника 2023-2025 (стр. 257):
Вспомните:
- Что называют функцией, ее область определения и область значений.
- Числовые промежутки.
- Свойства числовых неравенств.
- Равнобедренный треугольник.
- Высота и медиана равнобедренного треугольника.
- Параллельные прямые.
- Теорему Пифагора.
- Пропорции.
- Подобные треугольники.
- Первый признак подобия треугольников.
- Степень с натуральным показателем.
- Арифметический квадратный корень.
- Сокращение дробей.
- Десятичная запись дробных чисел.
- Умножение десятичных дробей.
№1146 учебника 2013-2022 (стр. 257):
Вспомните:
- Что называют функцией, ее график.
- Что называют корнем уравнения.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Деление рациональных чисел.
- Неправильные дроби.
- Смешанные числа.
- Подобные слагаемые.
- Дробные рациональные уравнения.
- Функция обратной пропорциональности.
Ответ
№1146 учебника 2023-2025 (стр. 257):
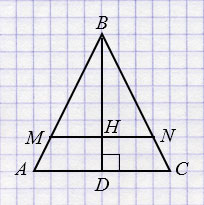
\(AB = BC = 5\) см, \(AC = 6\) см,
\(MN = y\) см, \(BH = x\) см.
\(BD\) - высота и медиана,
\(AD = DC = 3\) см.
1) По теореме Пифагора:
\( BD = \sqrt{AB^2 - AD^2} =\)
\(\sqrt{5^2 - 3^2} = \sqrt{25 - 9} = 4\) (см)
2) \(\triangle MBN \sim \triangle ABC\) по двум углам
(\(\angle B\) - общий, \(\angle A = \angle {BMN}\)), \(\Rightarrow \)
\(\frac{MN}{AC} = \frac{BH}{BD}\), \(\Rightarrow \)
\( \frac{y}{6} = \frac{x}{4}\)
\(4y = 6x\)
\(y = \frac64x = \frac32x = 1,5x\),
где \(0 < x \le 4\), тогда
\(1,5\cdot 0 < 1,5x \le 1,5 \cdot 4\)
\(0 < 1,5x \le 6\)
\(0 < y \le 6\)
Ответ: \(y = 1,5x\), \(E(y) = (0; 6]\).
Пояснения:
Равнобедренный треугольник - это треугольник, у которого боковые стороны равны. Высота равнобедренного треугольника является и его медианой, поэтому проведя высоту \(BD\) в \(\triangle ABC\) и учитывая то, что \(AD = DC = \frac12AC = 3\) см, по теореме Пифагора получим:
\( BD = \sqrt{AB^2 - AD^2} = 4\) (см)
Треугольники \( MBN\) и \(ABC\) подобны по двум углам (\(\angle B\) - общий, \(\angle A = \angle {BMN}\), как соответственные углы при пересечении параллельных прямых \(AC\) и \(MN\) секущей \(AM\)). В подобных треугольниках сходственные стороны пропорциональны, поэтому \(\frac{MN}{AC} = \frac{BH}{BD}\). Откуда, учитывая то, что \(MN = y\), \(BH = x\), \(AC = 6\), \(BD = 4\), имеем:
\( \frac{y}{6} = \frac{x}{4}\).
Тогда по свойству пропорции:
\(4y = 6x\), откуда \(y =1,5x\).
Подвижный отрезок может пройти расстояние от нуля до 4 см, так как \(BD = 4\) см, значит,
\(0 < x \le 4\), умножив части неравенства на \(1,5\), получим:
\(0 < 1,5x \le 6\), следовательно,
\(0 < y \le 6\), то есть область значений функции \(E(y) = (0; 6]\).
№1146 учебника 2013-2022 (стр. 257):
\(y = \dfrac{3x + 1}{x}\)
ОДЗ: \(x \ne0\).
а) \(x=0\) - не пересекает график функции, так как область определения функции все числа, кроме \(x\ne0\).
б) \(y=0\)
\(\dfrac{3x + 1}{x} = 0\)
\(3x + 1 = 0\)
\(3x = -1\)
\(x = -\dfrac{1}{3}\)
График функции пересекает прямую \(y=0\) в точке \(\left(-\dfrac{1}{3},0\right)\).
в) \(x=3\):
\( y = \dfrac{3\cdot3 + 1}{3} = \dfrac{10}{3} = 3\dfrac13\)
График функции пересекает прямую \(x=3\) в точке \((3,\dfrac{10}{3})\).
г) \(y=3\):
\(\dfrac{3x + 1}{x} = 3\) \(/\times x\)
\( 3x + 1 = 3x\)
\(\cancel{3x} + 1 - \cancel{3x}=0\)
\( 1 = 0\) - неверно.
График функции не пересекает прямую \(y=3\).
Пояснения:
Основные формулы и понятия:
Функция \(y = \dfrac{3x + 1}{x}\) может быть преобразована к виду:
\[ y = 3 + \dfrac{1}{x}. \]
Это гипербола, смещённая вверх на 3 единицы. Область определения — все \(x\), кроме \(x=0\).
а) Согласно области определения функции \(x \ne 0\), поэтому пересечений графика функции с прямой \(x=0\) нет.
б) Решив уравнение при \(y=0\), нашли корень этого уравнения \(x=-\dfrac{1}{3}\), значит, график функции пересекает прямую \(y=0\).
в) Подставляя значение \(x=3\) в формулу функции, получили \( y = 3\dfrac13\), значит, график функции пересекает прямую \(x=3\).
г) Решив уравнение при \(y=3\), получили неверное равенство, то есть уравнение не имеет корней, значит, график функции не пересекает прямую \(y=3\).
Вернуться к содержанию учебника