Теорема Пифагора

Теорема

Доказательство

Дано: прямоугольный треугольник, 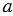и 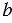- катеты, 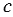- гипотенуза.

Доказать: .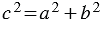

Доказательство:

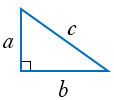
Достроим данный треугольник до квадрата со стороной + .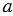

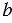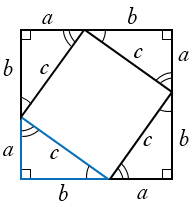
Площадь этого квадрата .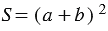

Также, по свойству 2⁰ площадей, площадь этого же квадрата 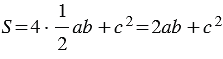, т.к. данный квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна 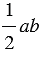, и внутреннего четырехугольника со стороной 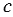, который является квадратом, так как каждый угол данного четырехугольника с парой острых углов из двух прямоугольных треугольников  образуют развернутый угол, т.е. равный 180⁰, при этом сумма пары острых углов равна 90⁰ (свойство прямоугольного треугольника), тогда угол внутреннего четырехугольника равен 180⁰ - 90⁰ = 90⁰. Следовательно, площадь квадрата со стороной  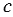равна .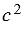

Итак, 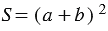и 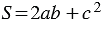, значит, 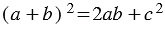, откуда 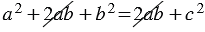, следовательно, 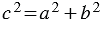. Теорема доказана.