Определение подобных треугольников
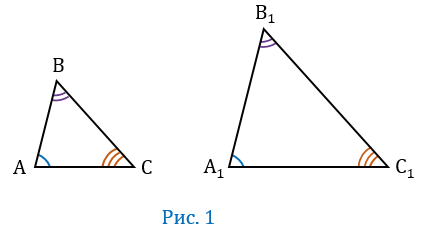
Пусть у 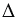 АВС и
АВС и 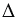 А1В1С1 углы соответственно равны:
А1В1С1 углы соответственно равны: 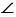 А =
А =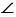 А1,
А1, 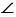 В =
В =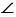 В1,
В1, 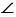 С =
С =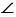 С1. Тогда стороны АВ и А1В1, ВС и В1С1, СА и С1А1 называются сходственными (Рис.1).
С1. Тогда стороны АВ и А1В1, ВС и В1С1, СА и С1А1 называются сходственными (Рис.1).
Определение
| Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. |
Треугольники АВС и А1В1С1 будут подобны, если
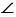 А =
А =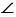 А1,
А1, 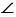 В =
В =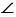 В1,
В1, 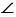 С =
С =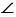 С1, (1)
С1, (1)
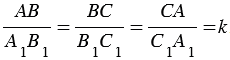 . (2)
. (2)
Число 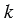 , равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом - 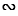 . На рисунке 1 треугольники АВС и А1В1С1 подобны, значит, можно записать:
. На рисунке 1 треугольники АВС и А1В1С1 подобны, значит, можно записать:
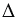 АВС
АВС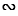
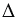 А1В1С1.
А1В1С1.
Советуем посмотреть:
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Правило встречается в следующих упражнениях:
7 класс
Задание 545, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 582, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 604, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 610, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1248, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1346, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 1146, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс