Упражнение 1150 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1150 учебника 2023-2025 (стр. 258):
Найдите нули функции (если они существуют):
а) \( y = \dfrac{2x + 11}{10};\)
б) \( y = \dfrac{6}{8 - 0{,}5x}; \)
в) \( y = \dfrac{3x^2 - 12}{4}. \)
№1150 учебника 2013-2022 (стр. 248):
Постройте график уравнения:
а) \(xy+3x=0\);
б) \((x-y)(y-5)=0\);
в) \((xy-6)(y-3)=0\);
г) \((x-y)^2+(x-1)^2=0\);
д) \(x^2-4=0\);
е) \(y^2-9=0\).
Подсказка
№1150 учебника 2023-2025 (стр. 258):
Вспомните:
- Что называют функцией, нули функции.
- Линейное уравнение с одной переменной.
- Деление и дроби.
- Десятичная запись дробных чисел.
- Деление рациональных чисел.
- Степень с натуральным показателем.
- Неполное квадратное уравнение.
- Арифметический квадратный корень.
№1150 учебника 2013-2022 (стр. 248):
Вспомните:
- Уравнение с двумя переменными.
- Линейная функция.
- Функция обратной пропорциональности.
- Разность квадратов двух выражений.
- Степень с натуральным показателем.
- Свойства умножения.
- Координаты точки на координатной плоскости.
- Деление и дроби.
- Деление рациональных чисел.
Ответ
№1150 учебника 2023-2025 (стр. 258):
а) \( y = \dfrac{2x + 11}{10} \)
\( \dfrac{2x + 11}{10} = 0 \)
\(2x + 11 = 0 \)
\(2x = -11 \)
\(x = -\dfrac{11}{2} \)
\(x= -5{,}5. \)
Ответ: \(y=0\) при \( x = -5{,}5. \)
б) \( y = \dfrac{6}{8 - 0{,}5x} \)
\(\dfrac{6}{8 - 0{,}5x} = 0 \) - невозможно, так как \(6 \ne 0\).
Ответ: нулей функции не существует.
в) \( y = \dfrac{3x^2 - 12}{4} \)
\( \dfrac{3x^2 - 12}{4} = 0 \)
\(3x^2 - 12 = 0\)
\( 3x^2 = 12\)
\( x^2 = \frac{12}{3}\)
\(x^2 = 4\)
\(x =\pm \sqrt4\)
\(x = \pm2\)
Ответ: \(y = 0\) при \( x = -2\) и \(x = 2. \)
Пояснения:
- Нулём функции называется значение аргумента \((x)\), при котором \(y = 0.\)
- Если функция имеет вид дроби, то нули возможны только в том случае, когда числитель равен нулю, а знаменатель при этом не обращается в ноль.
В пункте а) при приравнивании числителя к нулю, получили линейное уравнение \(2x + 11 = 0 \), которое имеет единственный корень \(x= -5{,}5\) - нуль функции.
В пункте б) числитель всегда отличен от нуля, значит, нулей функции не существует.
В пункте в) при приравнивании числителя к нулю, получили неполное квадратное уравнение \(3x^2 - 12 = 0\), которое имеет два корня: \( x_1 = -2\) и \(x_2 = 2 \) - нули функции.
№1150 учебника 2013-2022 (стр. 248):
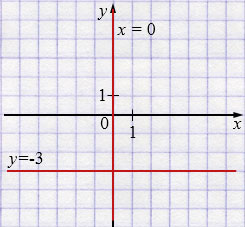
а) \(xy+3x=0\)
\(x(y+3)=0\)
\(x=0\) или \(y + 3 = 0\)
\( y=-3\)
б) \((x-y)(y-5)=0\)
\(x-y=0\) или \(y-5=0\)
\(y=x\) \(y=5\)
| \(x\) | \(0\) | \(3\) |
| \(y\) | \(0\) | \(3\) |

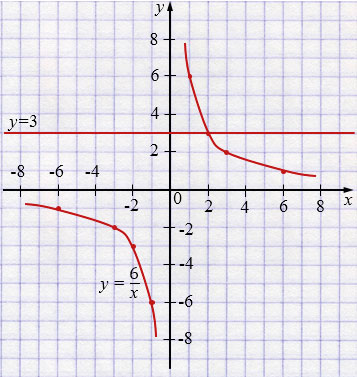
в) \((xy-6)(y-3)=0\)
\(xy-6=0\) или \(y-3=0\)
\(y=\dfrac{6}{x}\) \(y=3\).
\(y=\dfrac{6}{x}\) - гипербола.
| \(x\) | \(-6\) | \(-3\) | \(-2\) | \(-1\) |
| \(y\) | \(-1\) | \(-2\) | \(-3\) | \(-6\) |
| \(x\) | \(1\) | \(2\) | \(3\) | \(6\) |
| \(y\) | \(6\) | \(3\) | \(2\) | \(1\) |
г) \((x-y)^2+(x-1)^2=0\)
\(\begin{cases}x-y=0,\\ x-1=0 \end{cases}\)
\(\begin{cases} y=x,\\ x=1 \end{cases}\)
\(\begin{cases} y=1,\\ x=1 \end{cases}\)
График — точка \((1,1)\).

д) \(x^2-4=0\)
\((x-2)(x+2)=0\)
\(x-2=0\) или \( x+2=0\)
\(x=2\) \( x=-2\)

е) \(y^2-9=0\)
\((y-3)(y+3)=0\)
\(y-3=0\) или \(y+3=0\)
\(y=3\) \(y=-3\)

Пояснения:
Правило нулевого произведения.
\[AB=0 \;\Longleftrightarrow\; A=0 \text{ или } B=0.\] Если уравнение разложено на множители, график — объединение графиков уравнений каждого множителя \(=0\).
Сумма квадратов.
\[a^2+b^2=0 \;\Longleftrightarrow\; a=0 \text{ и } b=0,\] так как квадраты неотрицательны.
Частные типы графиков.
Линейные уравнения \(x=a\) и \(y=b\) задают, соответственно, вертикальные и горизонтальные прямые.
Из уравнения \(xy=c\,(c\ne0)\) получаем \(y=\dfrac{c}{x}\) (область определения: \(x\ne0\)), график — гипербола с асимптотами \(x=0\) и \(y=0\).
Комментарии к пунктам.
а) Группировка \(xy+3x=x(y+3)\) даёт две пересекающиеся прямые \(x=0\) и \(y=-3\) (пересечение \((0,-3)\)).
б) Произведение двух линейных множителей задаёт пару прямых: биссектриса первой и третьей координатной четвертей \(y=x\) и горизонтальная \(y=5\).
в) Один множитель задаёт гиперболу \(y=\dfrac{6}{x}\), другой — прямую \(y=3\); совместный график — их объединение.
г) Сумма квадратов равна нулю в единственной точке, где обе разности равны нулю: \((1,1)\). Значит, графиком является одна точка \((1,1)\).
д) Разложение разности квадратов даёт две параллельные вертикальные прямые \(x=\pm2\).
е) Разложение разности квадратов дает две параллельные горизонтальные прямые \(y=\pm3\).
Вернуться к содержанию учебника