Упражнение 717 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \( 9x^2-100=0 \)

\( 9x^2=100\)

\(x^2=\frac{100}{9} \)

\(x = \pm \sqrt{\frac{100}{9}} \)

\( x=\pm \frac{10}{3} \)

\( x=\pm 3\frac{1}{3} \)

Ответ: \(x=\pm 3\frac{1}{3}\).

б) \(2=7c^2\)

\(c^2=\frac{2}{7} \)

\( c=\pm \sqrt{\frac{2}{7}} \)

Ответ: \(c=\pm \sqrt{\frac{2}{7}}\).

в) \( 9m^2-4=0 \)

\(9m^2=4 \)

\(m^2=\frac{4}{9} \)

\(m = \pm \sqrt{\frac{4}{9}} \)

\[ m=\pm \frac{2}{3} \]

Ответ: \(m=\pm \frac{2}{3}\).

г) \( -0,8y^2+3y=0 \)

\( y(-0,8y+3)=0 \)

\( y=0 \)   или   \( -0,8y+3=0 \)

                       \( -0,8y=-3 \)

                        \(y=\frac{-3}{-0,8}\)

                       \(y=\frac{30}{8}\)

                       \(y=\frac{15}{4} \)

                       \(y=3\frac{3}{4} \)

Ответ: \(y=0, \; y=3\frac{3}{4}\).

Пояснения:

Корни уравнения не изменяются, если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

В пунктах а), б) и в) получилось неполное квадратное уравнение вида \(ax^2 = b\), откуда при \(a\neq0\) имеем \(x^2 = \frac{b}{a}\), тогда \(x_{1,2} = \pm\sqrt{\frac{b}{a}}\).

В пункте г) дано неполное квадратное уравнение \(ax^2+bx=0\), которое решается разложением на множители, учитывая то, что произведение равно нулю, когда хотя бы один из множителей равен нулю. При этом получается линейное уравнение вида \(ax = b\), которое при \(a\neq0\) имеет единственный корень \(x = \frac{a}{b}\).

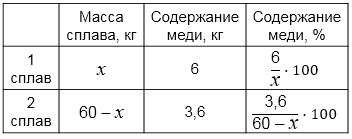
Составим уравнение:

\(\frac{6}{x}\cdot100 - \frac{3,6}{60-x}\cdot100=15\)

\(\frac{600}{x} - \frac{360}{60-x}=15\)   \(/\times x(60-x)\)

ОДЗ: \(x\neq0\)   и   \(60 - x\neq 0\)

                            \(x\neq60\)

\(600(60-x) - 360x=15x(60-x)\)

\(36000 - 600x - 360x= 900x - 15x^2\)

\(36000 - 600x - 360x- 900x + 15x^2=0\)

\(15x^2 -1860x + 36000=0\)   \( / :15\)

\(x^2 - 124x + 2400=0\)

\(a = 1\),  \(k = \frac b2 = -62\),  \(c =2400\)

\(D_1 = k^2 - ac =\)

\(=(-62)^2 - 1\cdot2400=\)

\(=3844 -2400=1444\),    \(\sqrt D = 38\).

\(x_{1,2} = \frac{-k \pm \sqrt D}{a}\)

\(x_1 = \frac{-(-62) + 38}{1} = 100\) - не удовлетворяет условию.

\(x_1 = \frac{-(-62) - 38}{1} = 24\)

1) \(24\) (кг) - масса первого сплава.

2) \(60 - 24 = 36\) (кг) - масса второго сплава.

Ответ: масса первого сплава — 24 кг, масса второго — 36 кг.

Пояснения:

Массу первого сплава обозначили через \(x\) кг, тогда масса второго равна \(60 - x\) кг.

Составили дробное рациональное уравнение, учитывая то, что первый сплав содержит 6 кг меди, а второй — 3,6 кг меди, при этом содержание меди в первом сплаве на 15% больше, чем во втором:

\(\frac{6}{x}\cdot100 - \frac{3,6}{60-x}\cdot100=15\).

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение с четным коэффициентом \(b\), у которого дискриминант \(D_1 = k^2 - 4ac>0\), где \(k = \frac b2\), поэтому уравнение имеет два корня: \(100\) и \(24\). Корень, равный \100\), не удовлетворяет условию задачи, так как масса одного сплава не может быть больше массы двух сплавов.

Значит, масса первого сплава равна 24 кг, а масса второго сплава:

\(60 - 24 = 36\) (кг).