Упражнение 698 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \( \begin{cases} y=x^{3},\\ xy=-12 \end{cases} \)

\( \begin{cases} y=x^{3},\\ y=-\frac{12}{x} \end{cases} \)

\(y=x^{3}\) - кубическая парабола, I и III четверти.

\(y=-\frac{12}{x}\) - гипербола, II и IV четвертях.

Ответ: система не имеет решений.

б) \( \begin{cases} y=x^{2}+8,\\ y=-x^2+12; \end{cases} \)

\(y=x^{2}+8\) - парабола, ветви направлены вверх, вершина \((0; 8)\).

\(y=-x^{2}+12\) - парабола, ветви направлены вниз, вершина \((0; 12)\).

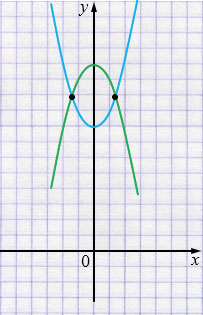
Ответ: система имеет два решения.

в) \( \begin{cases} y=x^{2}+1,\\ xy=3. \end{cases} \)

\( \begin{cases} y=x^{2}+1,\\ y=\frac3x. \end{cases} \)

\(y=x^{2}+1\) - парабола, ветви направлены вверх, вершина \((0; 1)\).

\(y=\frac3x\) - гипербола, I и III четверти.

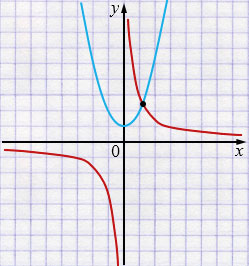
Ответ: система имеет одно решение.

Пояснения:

Суть графического метода решения системы уравнений с двумя переменными:

1) построить на одной координатной плоскости графики уравнений, входящих в систему;

2) найти координаты всех точек пересечения построенных графиков;

3) полученные пары чисел и будут искомыми решениями.

Пусть \(x\) км/ч скорость поезда по расписанию (\(x>0\)).

\(1 \;ч \;30\; мин = 1,5 \;ч = \frac32\; ч\)

Составим уравнение:

\( \frac{150}{x} + \frac32 + \frac{450}{x+15} = \frac{600}{x}\)  \(/\times2x(x+15)\)

ОДЗ: \(x \neq 0\)   и   \(x + 15 \neq 0\)

                            \(x \neq -15\)

\(300(x+15) +3x(x+15) + 900x = 1200(x + 15)\)   \(/ : 3\)

\(100(x+15) +x(x+15) + 300x = 400(x + 15)\)

\(100x + 1500 + x^2 +15x +300x = 400x + 6000\)

\(x^2 +415x +1500 - 400x - 6000 = 0\)

\(x^2 + 15x - 4500 = 0\)

\(a = 1\),  \(b = 15\),  \(c = -4500\)

\(D = b^2 - 4ac =\)

\(=15^2 - 4\cdot1\cdot(-4500)=\)

\(=225 + 18 000 = 18 225\).

\(\sqrt D = \sqrt {18 225} =\sqrt {25\cdot 729} =\)

\(=5 \cdot 27 =135\).

\( x_1=\frac{-15+135}{2}=\frac{120}{2}=60\)

\( x_2=\frac{-15-135}{2}=\frac{150}{2}=-75\) - не удовлетворяет условию.

1) \(60\) (км/ч) - скорость по расписанию.

2) \(\frac{600}{60}=10\) (ч)

Ответ: поезд был в пути \(10\) ч.

Пояснения:

Время в пути вычисляется по формуле \[t=\frac{S}{v}.\]

Мы ввели переменную \(x\) — первоначальную скорость поезда. Составили дробное рациональное уравнение, учитывая задержку и увеличение скорости:

\( \frac{150}{x} + \frac32 + \frac{450}{x+15} = \frac{600}{x}\)

Алгоритм решения дробного рационального уравнений:

1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;

2) найти общий знаменатель дробей, входящих в уравнение;

3) умножить обе части уравнения на общий знаменатель;

4) решить получившееся целое уравнение;

5) исключить из его корней те, которые совпадают с ОДЗ.

После того как обе части уравнения домножили на общий знаменатель и выполнили преобразования, получили квадратное уравнение, у которого дискриминант \(D = b^2 - 4ac>0\), поэтому уравнение имеет два корня: \(60\) и \(-75\). Но отрицательный корень не подходит, так как скорость не может быть отрицательным числом. Значит, скорость поезда по расписанию равна 60 км/ч.

Соответственно, общее время движения составило:

\(\frac{600}{60}=10\) (ч).