Упражнение 697 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№697 учебника 2023-2025 (стр. 164):
Решите графически систему уравнений \[ \begin{cases} y-x^{2}=0,\\ 2x-y+3=0. \end{cases} \]
№697 учебника 2013-2022 (стр. 156):
Найдите значения переменной \(y\), при которых:
а) сумма дробей \(\dfrac{6}{y+1}\) и \(\dfrac{y}{y-2}\) равна их произведению;
б) сумма дробей \(\dfrac{2}{y-3}\) и \(\dfrac{6}{y+3}\) равна их частному;
в) разность дробей \(\dfrac{y+12}{y-4}\) и \(\dfrac{y}{y+4}\) равна их произведению.
Подсказка
№697 учебника 2023-2025 (стр. 164):
Вспомните:
- Графический способ решения систем уравнений.
- Координаты точки.
- Квадратичная функция, ее график.
- Линейная функция, ее график.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
№697 учебника 2013-2022 (стр. 156):
Вспомните.
- Решение дробных рациональных уравнений.
- Рациональные дроби.
- Основное свойство рациональной дроби.
- Умножение и деление рациональных дробей.
- Решение полных квадратных уравнений (дискриминант).
- Что называют арифметическим квадратным корнем.
- Степень с натуральным показателем.
- Подобные слагаемые.
- Свойства уравнений.
- Линейное уравнение с одной переменной.
- Умножение одночлена на многочлен.
- Умножение многочлена на многочлен.
- Разность квадратов двух выражений.
- Квадрат суммы и квадрат разности двух выражений.
- Умножение рациональных чисел.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Деление рациональных чисел.
- Деление и дроби.
Ответ
№697 учебника 2023-2025 (стр. 164):
\( \begin{cases} y-x^{2}=0,\\ 2x-y+3=0. \end{cases} \)
\( \begin{cases} y=x^{2},\\ y=2x+3. \end{cases} \)
\(y=x^{2}\) - парабола.
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
\(y=2x+3\) - прямая.
| \(x\) | 0 | -2 |
| \(y\) | 3 | -1 |
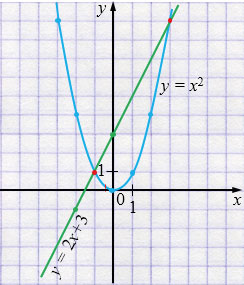
Ответ: \(\;(-1,\,1)\) и \((3,\,9)\).
Пояснения:
Суть графического метода решения системы уравнений с двумя переменными:
1) построить на одной координатной плоскости графики уравнений, входящих в систему;
2) найти координаты всех точек пересечения построенных графиков;
3) полученные пары чисел и будут искомыми решениями.
\(y = x^2\) - квадратичная функция, графиком которой является парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
\(y=kx+b\) - линейная функция, графиком которой является прямая. Для построения прямой достаточно двух точек.
№697 учебника 2013-2022 (стр. 156):
а) \(\dfrac{6}{y+1}+\dfrac{y}{y-2}=\dfrac{6}{y+1}\cdot\dfrac{y}{y-2}\)
\(\dfrac{6}{y+1}+\dfrac{y}{y-2}=\dfrac{6y}{(y+1)(y-2)}\) \(/\times(y+1)(y-2)\)
ОДЗ:
\(y + 1 \neq 0\) и \(y - 2 \neq 0\)
\(y \neq -1\) \(y \neq 2\)
\(6(y-2) + y(y+1) = 6y\)
\(6y - 12 + y^2 + y - 6y = 0\)
\(y^2 +y-12 = 0\)
\(a = 1\), \(b = 1\), \(c = -12\)
\(D = b^2 - 4ac = 1^2 - 4\cdot1\cdot(-12) = \)
\( = 1 + 48 = 49\), \(\sqrt D = 7\).
\(y_1=\dfrac{-1 + 7}{2\cdot1}=\dfrac62=3\).
\(y_2=\dfrac{-1 - 7}{2\cdot1}=\dfrac{-8}{2}=-4.\)
Ответ: \(y=3, \; -4.\)
б) \(\dfrac{2}{y-3}+\dfrac{6}{y+3}=\dfrac{2}{y-3} : \dfrac{6}{y+3}\)
\(\dfrac{2}{y-3}+\dfrac{6}{y+3}=\dfrac{\cancel2}{y-3} \cdot \dfrac{y+3}{\cancel6_3}\)
\(\dfrac{2}{y-3}+\dfrac{6}{y+3}=\dfrac{y+3}{3(y-3)}\) \(/\times 3(y+3)(y-3)\)
ОДЗ:
\(y + 3 \neq 0\) и \(y - 3 \neq 0\)
\(y \neq -3\) \(y \neq 3\)
\(6(y + 3) +18(y-3) = (y+3)^2\)
\(6y + 18 +18y - 54 = y^2 +6y + 9\)
\(6y + 18 +18y - 54 - y^2 -6y - 9=0\)
\(-y^2 + 18y - 45 = 0\) \(/\times(-1)\)
\(y^2 - 18y + 45 = 0\)
\(a = 1\), \(b = -18\), \(c = 45\)
\(D = b^2 - 4ac =\)
\(=(-18)^2 - 4\cdot1\cdot45=\)
\(= 324 + 180 = 144,\) \(\sqrt D = 12\).
\(y_1=\dfrac{-(-18) + 12}{2\cdot1}=\dfrac{30}{2}=15\).
\(y_2=\dfrac{-(-18) - 12}{2\cdot1}=\dfrac{6}{2}=3\) - не подходит по ОДЗ.
Ответ: \(y=15.\)
в) \(\dfrac{y+12}{y-4}-\dfrac{y}{y+4}=\dfrac{y+12}{y-4}\cdot\dfrac{y}{y+4}\)
\(\dfrac{y+12}{y-4}-\dfrac{y}{y+4}=\dfrac{y(y+12)}{(y-4)(y+4)}\) \(/\times (y-4)(y+4)\)
ОДЗ:
\(y - 4 \neq 0\) и \(y + 4 \neq0\)
\(y \neq 4\) \(y \neq -4\)
\((y + 12)(y+4) - y(y-4) = y(y + 12)\)
\(\cancel{y^2} + 4y + 12y + 48 - \cancel{y^2} +4y = y^2 + 12y\)
\(4y + \cancel{12y} + 48+4y - y^2 - \cancel{12y} = 0\)
\(-y^2 + 8y + 48 = 0\) \(/\times(-1)\)
\(y^2 - 8y - 48 = 0\)
\(a = 1\), \(b = -8\), \(c = -48\)
\(D = b^2 - 4ac =\)
\(=(-8)^2 -4\cdot1\cdot(-48)=\)
\(= 64 + 192 = 256\), \(\sqrt D = 16\).
\(y_1=\dfrac{-(-8) + 16}{2\cdot1}=\dfrac{24}{2}=12\).
\(y_2=\dfrac{-(-8) - 16}{2\cdot1}=\dfrac{-8}{2}=-4\) - не подходит по ОДЗ.
Ответ: \(y=12.\)
Пояснения:
В каждом случае по условию составили дробное рациональное уравнение.
Алгоритм решения уравнений:
1) найти ОДЗ (область допустимых значений), то есть те значения переменной, при которых знаменатель обращается в нуль;
2) найти общий знаменатель дробей, входящих в уравнение (предварительно, если возможно, разложить все знаменатели на множители);
3) умножить обе части уравнения на общий знаменатель;
4) решить получившееся целое уравнение;
5) исключить из его корней те, которые совпадают с ОДЗ.
Решение целых уравнений:
1) Полное квадратное уравнение \(ax^2 + bx + c=0\), которое решается через дискриминант \(D = b^2-4ac\).
– если \(D>0\), то уравнение имеет два корня:
\(x_1 =\frac{-b+\sqrt{D}}{2a}\);
\(x_2 =\frac{-b-\sqrt{D}}{2a}\).
– если \(D=0\), то уравнение имеет один корень:
\(x=-\frac {b}{2a}\).
2) Линейное уравнение вида \(ax = b\), которое при \(a\neq0\) имеет единственный корень \(x = \frac{a}{b}\).
Разность квадратов:
\(a^2 - b^2 = (a-b)(a + b)\).
Квадрат суммы двух выражений:
\((a +b)^2 = a^2 + 2ab +b^2\).
Вернуться к содержанию учебника