Наименьшее общее кратное

Задача:

Петя строит железную дорогу из частей, длина которых 4 см, а Сережа, из частей длина которых 6 см. Какую наименьшую протяженность дорожного полотна построят мальчики равной длины?

Решение:

Длина дороги, построенной мальчиками, должна делиться нацело на 4 и 6, так как части, из которых строят дорогу Петя и Сережа равны 4 см и 6 см соответственно, то есть длина построенной железной дороги должна быть кратной и 4, и 6.

Числа кратные 4:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...

Числа кратные 6:

6, 12, 18, 24, 30, 36, 42, 48, 54, 60...

То есть общими кратными чисел 4 и 6 являются числа (выделено синим):

12, 24, 36, 48, 60...

Но наименьшим из них является 12. Это число называется наименьшим общим кратным.

То есть наименьшая протяженность дорожного полотна равной длины у Пети и Сережи 12 см.

Наименьшее общее кратное чисел 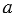и 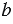обозначают так: НОК(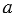; 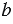), то есть мы можем записать НОК(4; 6) = 12.

Нахождение наименьшего общего кратного:

1 способ:

Найдем НОК(12; 15).

Выбираем наибольшее из двух чисел, в нашем случае это число 15, и записываем числа кратные ему, до тех пор, пока не получим число, которое будет кратно второму числу, в нашем случае числу 12.

Получаем: 15, 30, 45, 60.

Число 60 является наименьшим общим кратным чисел 12 и 15, то есть НОК(12; 15) = 60.

2 способ:

Разложим данные числа на простые множители:

12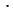 = 22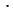3          15 = 3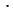5.

Далее для выписываем простые множители, которые входят в разложение первого числа, и добавляем множители из разложения второго числа, которых нет в разложении первого, то есть в нашем случае, это множитель 5.

Итак, мы получим 4 множителя 2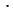235, произведение данных множителей равно числу 60, которое является наименьшим общим кратным чисел 12 и 15, то есть мы снова получили НОК(12; 15) = 60.

Таким же образом можно найти НОК трех и более чисел.

Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.

3 способ:

Найдем НОК(2520; 4620). Для это разложим данные числа на простые множители и запишем разложение в виде произведения степеней:

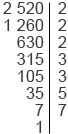
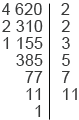
2 520 = 2³3²5¹7¹                            4 620 = 2²3¹5¹7¹11¹.

Далее используем правило:

В нашем случае:

1. Встречается только в одном разложении: 11¹.
2. Степени с бóльшими показателями: 2³, 3², 5¹, 7¹.
3. Находим произведение данных степеней, то есть искомый наименьшее общее кратное:  НОК(2520; 4620) = 2³3²5¹7¹11 = 27 720.