Приведение дробей к общему знаменателю
Если мы умножим числитель и знаменатель дроби  на одно и то же число 3, то получим дробь
на одно и то же число 3, то получим дробь 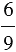 , равную данной, то есть
, равную данной, то есть 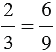 , в данном случае принято говорить, что мы дробь
, в данном случае принято говорить, что мы дробь  привели к новому знаменателю 9.
привели к новому знаменателю 9.
Дополнительный множитель - это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель. При этом при приведении дроби к новому знаменателю используем основное свойство дроби и умножаем её числитель и знаменатель на дополнительный множитель. Чтобы найти дополнительный множитель необходимо новый знаменатель разделить на данный.
Например: Приведем дробь 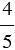 к знаменателю 40. Для этого найдем дополнительный множитель, поделив 40 на 5, получим, что дополнительный множитель равен 40 : 5 = 8.
к знаменателю 40. Для этого найдем дополнительный множитель, поделив 40 на 5, получим, что дополнительный множитель равен 40 : 5 = 8.
Далее воспользуемся основным свойством дроби, найдем:
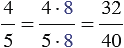 .
.
Рассмотрим дроби 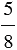 и
и 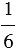 . Мы видим что данные дроби имеют разные знаменатели, но с помощью основного свойства дроби мы можем их привести к одному знаменателю, другими словами к общему знаменателю.
. Мы видим что данные дроби имеют разные знаменатели, но с помощью основного свойства дроби мы можем их привести к одному знаменателю, другими словами к общему знаменателю.
Например, общим знаменателем для данных дробей будет знаменатель, равный произведению данных знаменателей, то есть 8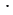 6 = 48. Чтобы привести дробь
6 = 48. Чтобы привести дробь 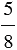 к знаменателю 48, необходимо умножить ее числитель и знаменатель на дополнительный множитель 6, а знаменатель и числитель дроби
к знаменателю 48, необходимо умножить ее числитель и знаменатель на дополнительный множитель 6, а знаменатель и числитель дроби 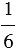 - на дополнительный множитель 8. Имеем:
- на дополнительный множитель 8. Имеем:
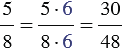 и
и 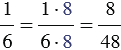 .
.
Мы привели дроби 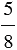 и
и 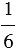 к общему знаменателю 48. Заметим, что общий знаменатель дробей всегда должен быть кратным, каждому из данных знаменателей.
к общему знаменателю 48. Заметим, что общий знаменатель дробей всегда должен быть кратным, каждому из данных знаменателей.
| Общий знаменатель дробей - это общее кратное их знаменателей. |
Обычно принято приводить дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю используем правило:
|
- В нашем примере НОК (6; 8) = 24, то есть наименьшим общим знаменателем наших дробей является 24.
- Находим дополнительные множители: для дроби
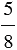 - это число 24 : 8 = 3, а для дроби
- это число 24 : 8 = 3, а для дроби 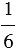 - число 24 : 6 = 4.
- число 24 : 6 = 4. - Умножаем числитель и знаменатель каждой дроби на её дополнительный множитель:
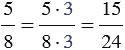 и
и 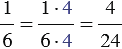 .
.
Обычно принято, дополнительный множитель писать над числителем справа, то есть наша запись будет иметь вид:
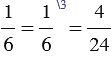 и
и 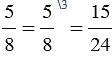 .
.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 5.395, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.417, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.449, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.59, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.66, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.234, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6.239, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.478, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.481, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.483, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 298, Мерзляк, Полонский, Якир, Учебник
Номер 896, Мерзляк, Полонский, Якир, Учебник
Номер 1009, Мерзляк, Полонский, Якир, Учебник
Задание 403, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 418, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 500, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.231, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.26, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.77, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.113, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 47, Мерзляк, Полонский, Якир, Учебник
Номер 48, Мерзляк, Полонский, Якир, Учебник
Номер 430, Мерзляк, Полонский, Якир, Учебник
Номер 493, Мерзляк, Полонский, Якир, Учебник
Номер 527, Мерзляк, Полонский, Якир, Учебник
Номер 845, Мерзляк, Полонский, Якир, Учебник
Номер 1156, Мерзляк, Полонский, Якир, Учебник
Упражнение 76, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 149, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 135, Мерзляк, Полонский, Якир, Учебник
Номер 201, Мерзляк, Полонский, Якир, Учебник
Упражнение 853, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 938, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 952, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 953, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 955, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1263, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1274, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 268, Макарычев, Миндюк, Учебник
9 класс