Делители и кратные
Попробуйте раздать поровну 15 тетрадей трем одноклассникам.
Это сделать легко, каждый получит по 5 тетрадей.



Но на шестерых одноклассников все 15 тетрадей разделить поровну нельзя.
Каждому достанется по две тетради и три тетради окажутся лишними.





 +
+ 
Говорят, что число 15 кратно трем, а число 3 является делителем числа 15. Число 15 имеет четыре делителя: 1, 3, 5, 15.
Число 1 является делителем любого натурального числа.
Любое натуральное число имеет бесконечно много кратных.
Например, число три является кратным (является делителем) таких чисел, как, 3, 6, 9, 12, 15, 18, 21 ,...
(Здесь только первые 7 чисел натурального ряда, кратных трем (делятся на 3 без остатка). Продолжать можно до бесконечности.
Произносите правильно:
число 15 кратно трем (делится без остатка на 3); число 15 кратное числа три; число три является делителем числа 15.
Запомните:
Делителем натурального числа n называют натуральное число, на которое n делится без остатка.
Например, число 3 называется делителем числа 18, так как число 18 делится на 3 без остатка.
18 : 3 = 6
Кратным натурального числа n называют натуральное число, которое делится на n без остатка.
Например, число 36 называется кратным числа 4 (36 кратно четырем), так как 36 делится на 4 без остатка.
36 : 4 = 9
Вообще, для любого натурального числа 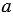 каждое из чисел
каждое из чисел 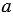
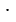 1,
1, 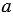
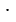 2,
2, 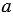
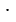 3,
3, 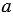
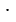 4, ... является кратным числа
4, ... является кратным числа 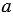 .
.
Наименьшим из кратных натурального числа является само это число.
Свойства:
1) Если каждое из чисел 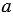 и и 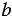 делится нацело на число делится нацело на число 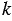 , то и сумма , то и сумма 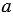 + + 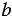 также делится нацело на число также делится нацело на число 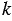 . . |
Пример: 15 : 5 = 3 и 35 : 5 = 7, а 15 + 35 = 50 и 50 : 5 = 10.
2) Если ни число 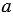 и ни число и ни число 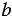 не делятся нацело на число не делятся нацело на число 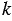 , то сумма , то сумма 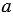 + + 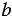 может делиться, а может и не делиться нацело на число может делиться, а может и не делиться нацело на число 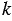 . . |
Примеры:
1) 13 и 7 не делятся на 5, а их сумма 13 + 7 = 20 делится на 5 (20 : 5 = 4).
2) 11 и 6 не делятся на 4 и их сумма 11 + 6 = 17 не делится на 4.
3) Если число 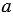 делится нацело на число делится нацело на число 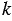 , а число , а число 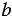 не делится нацело на число не делится нацело на число 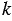 , то сумма , то сумма 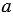 + + 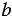 не делится нацело на число не делится нацело на число 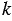 . . |
Пример: 15 + 25 = 40, слагаемое 15 и сумма 40 делятся нацело на 5 и также слагаемое 25 делится нацело на 5.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 5.367, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.368, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.79, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 3.338, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.340, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.344, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.346, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.347, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.425, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 10, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 174, Мерзляк, Полонский, Якир, Учебник
Номер 176, Мерзляк, Полонский, Якир, Учебник
Номер 257, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Задание 12, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 350, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 586, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 2.7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 57, Мерзляк, Полонский, Якир, Учебник
Номер 336, Мерзляк, Полонский, Якир, Учебник
Номер 519, Мерзляк, Полонский, Якир, Учебник
Номер 552, Мерзляк, Полонский, Якир, Учебник
Номер 674, Мерзляк, Полонский, Якир, Учебник
Номер 696, Мерзляк, Полонский, Якир, Учебник
Номер 1180, Мерзляк, Полонский, Якир, Учебник
Упражнение 744, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 791, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 967, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 194, Мерзляк, Полонский, Якир, Учебник
Номер 204, Мерзляк, Полонский, Якир, Учебник
Номер 370, Мерзляк, Полонский, Якир, Учебник
Номер 421, Мерзляк, Полонский, Якир, Учебник
Номер 453, Мерзляк, Полонский, Якир, Учебник
Номер 615, Мерзляк, Полонский, Якир, Учебник
Упражнение 70, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 209, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 447, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 907, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс