Наибольший общий делитель

Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.

Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.

Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.

Наибольший общий делитель чисел 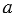и 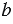обозначают так: НОД(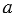; 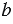), то есть мы можем записать НОД(36; 126) = 18.

Предварительно разложив числа на простые множители, мы упростим нахождение наибольшего общего делителя многозначных чисел.

Найдем НОД(240; 165).

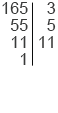
240 = 222235                       165 = 3511.

Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.

Найдем НОД(2520; 4620).

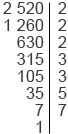
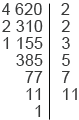
2 520 = 2223357                 4 620 = 2235711.

Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 - дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520. Так же число 3 является множителем рассматриваемых чисел, а число 9 = 33 является только делителем числа 2520. Кроме чисел 4 и 3, общими делителями данных чисел являются числа 5 и 7.

Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357  рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.

Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).

Таким же образом можно найти НОД трех и более чисел.

Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.

Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:

2 520 = 2³3²5¹7¹

4 620 = 2²3¹5¹7¹11¹.

Тогда НОД мы можем найти по следующему правилу:

 Найдем НОД(2520; 4620):

1.  Выписываем общие основания: 2, 3, 5, 7.
2. Выбираем наименьшие показатели данных степеней: 2², 3¹, 5¹, 7¹.
3. Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 2²3¹5¹7¹ = 420.