Сравнение дробей
Сравнить две дроби - это значит установить, какая из них больше, а какая меньше.
| Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше. |
Пример:
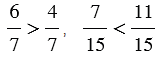 .
.
Чтобы сравнить дроби с разными знаменателями, нужно привести их к общему знаменателю.
Пример: Сравним дроби: 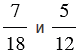 .
.
Наименьший общий знаменатель данных дробей равен 36. Приведем каждую из дробей к общему знаменателю, для этого найдем к каждой из дробей дополнительный множитель. Для первой дроби дополнительный множитель - 2, т.к. 18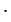 2 = 36, а для второй дроби дополнительный множитель - 3, т.к. 12
2 = 36, а для второй дроби дополнительный множитель - 3, т.к. 12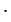 3 = 36. Получим:
3 = 36. Получим:
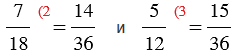 .
.
По правилу сравнения дробей с одинаковыми знаменателями 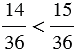 , значит, и
, значит, и 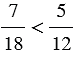 .
.
| Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, а меньше та, у которой знаменатель больше. |
Пример:
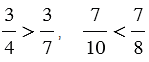 .
.
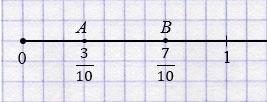
| На координатном луче из двух дробей большая расположена правее меньшей. |
Пример:
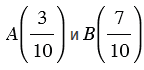 .
.
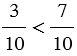 , значит, точка А лежит левее точки В (смотри рисунок ниже).
, значит, точка А лежит левее точки В (смотри рисунок ниже).
|
Если числитель дроби равен знаменателю, то дробь равна единице, т.е. |
Пример:
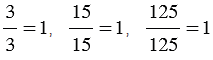 .
.
| Любая правильная дробь меньше единицы, а любая неправильная дробь больше или равна единице. |
Пример:
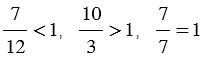 .
.
| Каждая неправильная дробь больше любой правильной, а каждая правильная дробь меньше любой неправильной дроби. |
Пример:
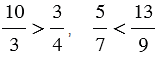 .
.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 942, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1026, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1029, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1167, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1726, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 5.109, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание стр. 73, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.14, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.102, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 1, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 215, Мерзляк, Полонский, Якир, Учебник
Номер 255, Мерзляк, Полонский, Якир, Учебник
Номер 256, Мерзляк, Полонский, Якир, Учебник
Задание 172, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1113, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1498, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.92, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.157, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.437, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание П.104, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 25, Мерзляк, Полонский, Якир, Учебник
Упражнение 8, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 66, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 68, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 69, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 76, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 84, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 127, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 210, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1221, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 252, Мерзляк, Полонский, Якир, Учебник
Номер 253, Мерзляк, Полонский, Якир, Учебник
Номер 254, Мерзляк, Полонский, Якир, Учебник
Номер 902, Мерзляк, Полонский, Якир, Учебник
Упражнение 54, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 467, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1113, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1280, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 269, Макарычев, Миндюк, Учебник
Упражнение 270, Макарычев, Миндюк, Учебник
9 класс
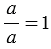 , где
, где 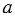 -
-