Простые и составные числа
Любое натуральное число, за исключением 1, имеет как минимум два делителя (единица имеет единственный делитель - единицу) - это единица и само это число. Пусть 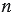 - данное натуральное число, действительно, для него мы можем записать, что
- данное натуральное число, действительно, для него мы можем записать, что 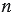 : 1 =
: 1 = 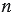 и
и 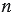 :
: 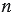 = 1.
= 1.
Некоторые числа имеют только два делителя - единицу и само это число, примером такого число является 11, это число делится только на 1 и на 11. Также только два делителя имеют, например, числа 2, 3, 5, 7, 13, 17. Все такие числа называют простыми числами.
| Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число. |
Наименьшим простым числом является 2, при этом оно единственное чётное простое число, так как все остальные чётные числа делятся не только на себя и единицу, но и на 2, то есть имеют минимум 3 делителя.
Число простых чисел бесконечно, и хотя не известен алгоритм их нахождения.
| Натуральное число называют составным, если оно имеет больше двух натуральных делителей. |
Наименьшим составным числом является 4, оно имеет три делителя: 1, 2, 4.
Число составных чисел бесконечно. При этом любое составное число можно разложить на два множителя, каждый из которых больше 1. Например, рассмотрим число 186:
186 : 6 = 31, значит, 186 = 6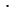 31.
31.
Говорят, что число 186 на разложено на множители 6 и 31.
Обратите внимание, что 1 не относят ни к составным числам, ни к простым, так как оно имеет только один делитель.
Советуем посмотреть:
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 9 и на 3
Разложение на простые множители
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Правило встречается в следующих упражнениях:
5 класс
Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 5.435, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 105, Мерзляк, Полонский, Якир, Учебник
Номер 110, Мерзляк, Полонский, Якир, Учебник
Номер 123, Мерзляк, Полонский, Якир, Учебник
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 1213, Мерзляк, Полонский, Якир, Учебник
Задание 189, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 9, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.70, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.76, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.124, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 349, Мерзляк, Полонский, Якир, Учебник
Номер 555, Мерзляк, Полонский, Якир, Учебник
Номер 848, Мерзляк, Полонский, Якир, Учебник
Упражнение 515, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 516, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 519, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 520, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 521, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 522, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 916, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 376, Мерзляк, Полонский, Якир, Учебник
Номер 444, Мерзляк, Полонский, Якир, Учебник
Номер 453, Мерзляк, Полонский, Якир, Учебник
Номер 456, Мерзляк, Полонский, Якир, Учебник
Упражнение 396, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 397, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 898, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 900, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 907, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1036, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс