Номер 615 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 150

Ответ: число 2 записано на третьем месте.

Пояснения:

Натуральные числа от 1 до 37 записаны в строку так, что сумма любых первых нескольких чисел делится нацело на следующее за ними число. Какое число записано на третьем месте, если на первом месте записано число 37, а на втором - 1?

Запишем сумму чисел, записанных в строку:

1 + 2 + ...+ 35 + 36 + 37.

Числа 1 и 36 дают в сумме 37, числа 2 и 35 также дает в сумме 37, и в данной сумме имеется 18 таких пар и число 37, то есть получаем, что наша сумма равна 37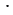18 + 37 = 37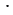19.

По условию на первом месте записано число 37, а на втором - 1, при этом их сумма должна делится на число, которое стоит на третьем месте, то есть число 37 + 1 = 38, должно делится на число, записанное на третьем месте. Число 38 имеет три делителя, которые расположены от 1 до 37, это числа 1, 2 и 19. Число 1 не подходит, так как оно записано на втором месте, то есть у нас остается число 2 и число 19.

Заметим, что на последнее число, стоящее в строке,  должна делиться сумма чисел в строке, кроме данного числа. Выше мы нашли, что сумма чисел равна 37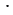19, а так как число 37 находится на первом месте, то на последнем месте может находится только число 19, тогда на третьем месте может находится только число 2.